Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cunningham, F.
1966.
Generalization of a theorem of P. D. Finch's on integration of set-functions.
Journal of the Australian Mathematical Society,
Vol. 6,
Issue. 4,
p.
460.
Bolker, Ethan D.
1966.
Functions resembling quotients of measures.
Transactions of the American Mathematical Society,
Vol. 124,
Issue. 2,
p.
292.


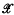 be a space of points
be a space of points 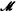 a σ-field of subsets of
a σ-field of subsets of 