Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T09:25:24.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Functional least squares estimators in an additive effects outliers model

Part of: Inference from stochastic processes Nonparametric inference

Published online by Cambridge University Press:  09 April 2009

Sunil K. Dhar
Sunil K. Dhar
Affiliation:
Department of MathematicsThe University of AlabamaP.O. Box 870350 Tuscaloosa, Alabama 35487-0350, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

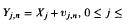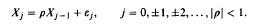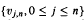Consider the additive effects outliers (A.O.) model where one observes , with The sequence of r.v.s is independent of and 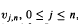, are i.i.d. with d.f. 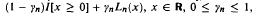, where the d.f.s Ln, n ≦ 0, are not necessarily known and εj's are i.i.d.. This paper discusses the asymptotic behavior of functional least squares estimators under the above model. Uniform consistency and uniform strong consistency of these estimators are proven. The weak convergence of these estimators to a Gaussian process and their asymptotic biases are also discussed under the above A.O. model.

MSC classification

Secondary: 62G05: Estimation 62M10: Time series, auto-correlation, regression, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 48 , Issue 2 , April 1990 , pp. 299 - 319
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Ash, R. B., Real analysis and probability (Academic Press, New York, 1972).Google Scholar
[2]Billingsley, P., Convergence of probability measure (Wiley New York, 1968).Google Scholar
[3]Chung, K. L., A course in probability theory, 2nd ed. (Academic Press, New York, 1974).Google Scholar
[4]Csörgö, S., ‘The theory of functional least squares’, J. AustraL Math. Soc. Ser. A 34 (1983), 336–355.Google Scholar
[5]Denby, L. and Martin, D., ‘Robust estimation of the first order autoregressive parameter’, J. Amer. Statist. Assoc. 74 (365) (1979), 140–146.CrossRefGoogle Scholar
[6]Gaenssler, P. and Stute, W., On uniform convergence of measures with applications to uniform convergence of empirical distributions, (Lecture Notes in Math. 566, 1976).Google Scholar
[7]Heathcote, C. R. and Welsh, A. H., ‘The robust estimation of auto-regressive processes by functional least squares’, J. Appl. Prob. 20 (1983), 737–753.Google Scholar
[8]Ibragimov, I. A. and Linnik, Y. V., Independent and stationary sequences of random variables (Wolters-Noordhoff, Groningen, 1971).Google Scholar
[9]Martin, D. and Yohai, V. J., ‘Influence functionals for time series’, Ann. Statist. 14 (3) (1986), 781–818.Google Scholar
[10]Pham, T. D. and Tran, L. T., ‘Some mixing properties of time series models’, Stochastic Processes Appl. 19 (1985), 297–303.Google Scholar
[11]Stute, W. and Schumann, G., ‘A general Glivenko-Cantelli theorem for stationary sequences of random observations’, Scand. J. Statist. 7 (1980), 102–104.Google Scholar
[12]Withers, C. S., ‘Central limit theorems for dependent variables. I’, Z. Wahrsch. Verw. Gebiete 57 (1981), 509–534.CrossRefGoogle Scholar
[13]Withers, C. S., ‘Corrigendum to central limit theorems for dependent variables. I’, Z. Wahrsch. Verw. Gebiete 63 (1983), 555.CrossRefGoogle Scholar