Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-08T18:34:09.507Z Has data issue: false hasContentIssue false
  • English
  • Français

FREELY QUASICONFORMAL MAPS AND DISTANCE RATIO METRIC

Part of: Riemann surfaces Geometric function theory

Published online by Cambridge University Press:  09 September 2014

YAXIANG LI ,
SAMINATHAN PONNUSAMY  and
MATTI VUORINEN
YAXIANG LI
Affiliation:
College of Science, Central South University of Forestry and Technology, Changsha, Hunan 410004, PR China email [email protected]
SAMINATHAN PONNUSAMY*
Affiliation:
Indian Statistical Institute (ISI) Chennai Centre, SETS (Society for Electronic Transactions and Security), MGR Knowledge City, CIT Campus, Taramani, Chennai 600 113, India email [email protected], [email protected]
MATTI VUORINEN
Affiliation:
Department of Mathematics and Statistics, University of Turku, FIN-20014 Turku, Finland email [email protected]
*
✉[email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 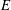$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$ and 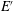$E'$ denote real Banach spaces with dimension at least 2 and that 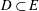$D\subset E$ and $D'\subset E'$ are domains. Let 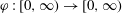$\varphi :[0,\infty )\to [0,\infty )$ be a homeomorphism with 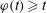$\varphi (t)\geq t$. We say that a homeomorphism 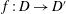$f: D\to D'$ is 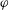$\varphi $-FQC if for every subdomain 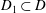$D_1 \subset D$, we have 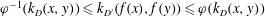$\varphi ^{-1} (k_D(x,y))\leq k_{D'} (f(x),f(y))\leq \varphi (k_D(x,y))$ holds for all 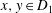$x,y\in D_1$. In this paper, we establish, in terms of the 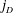$j_D$ metric, a necessary and sufficient condition for a homeomorphism 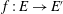$f: E \to E'$ to be FQC. Moreover, we give, in terms of the 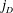$j_D$ metric, a sufficient condition for a homeomorphism 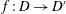$f: D\to D'$ to be FQC. On the other hand, we show that this condition is not necessary.

Keywords

quasihyperbolic metricquasiconformal mappingFQC mappingdistance ratio metric

MSC classification

Secondary: 30C65: Quasiconformal mappings in $^n$, other generalizations 30F45: Conformal metrics (hyperbolic, Poincaré, distance functions) 30C20: Conformal mappings of special domains
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 383 - 390
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Anderson, G. D., Vamanamurthy, M. K. and Vuorinen, M., ‘Dimension-free quasiconformal distortion in n-space’, Trans. Amer. Math. Soc. 297 (1986), 687–706.Google Scholar
Gehring, F. W. and Osgood, B. G., ‘Uniform domains and the quasi-hyperbolic metric’, J. Anal. Math. 36 (1979), 50–74.Google Scholar
Gehring, F. W. and Palka, B. P., ‘Quasiconformally homogeneous domains’, J. Anal. Math. 30 (1976), 172–199.CrossRefGoogle Scholar
Hästö, P., Ibragimov, Z., Minda, D., Ponnusamy, S. and Sahoo, S. K., ‘Isometries of some hyperbolic-type path metrics, and the hyperbolic medial axis. In the tradition of Ahlfors–Bers, IV’, Contemp. Math. 432 (2007), 63–74.Google Scholar
Heinonen, J., Lectures on Analysis on Metric Spaces (Springer, New York, 2001).Google Scholar
Huang, M., Ponnusamy, S., Wang, H. and Wang, X., ‘A cosine inequality in hyperbolic geometry’, Appl. Math. Lett. 23 (2010), 887–891.Google Scholar
Kauhanen, J., Koskela, P. and Malý, J., ‘Mappings of finite distortion: discreteness and openness’, Arch. Ration. Mech. Anal. 160 (2001), 135–151.Google Scholar
Klén, R., ‘Local convexity properties of quasihyperbolic balls in punctured space’, J. Math. Anal. Appl. 342 (2008), 192–201.Google Scholar
Klén, R., ‘On hyperbolic type metrics’, Dissertation, University of Turku. Ann. Acad. Sci. Fenn. Math. Diss. 152 (2009), 49 pp.Google Scholar
Klén, R., Rasila, A. and Talponen, J., ‘Quasihyperbolic geometry in Euclidean and Banach spaces’, J. Anal. 18 (2010), 261–278.Google Scholar
Rasila, A. and Talponen, J., ‘Convexity properties of quasihyperbolic balls on Banach spaces’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 37 (2012), 215–228.Google Scholar
Rasila, A. and Talponen, J., ‘On quasihyperbolic geodesics in Banach spaces’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 39 (2014), 163–173.Google Scholar
Tukia, P. and Väisälä, J., ‘Quasisymmetric embeddings of metric spaces’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 5 (1980), 97–114.CrossRefGoogle Scholar
Väisälä, J., Lectures on n-Dimensional Quasiconformal Mappings, Lecture Notes in Mathematics, 229 (Springer, Berlin–New York, 1971).Google Scholar
Väisälä, J., ‘Free quasiconformality in Banach spaces I’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 15 (1990), 355–379.Google Scholar
Väisälä, J., ‘Free quasiconformality in Banach spaces II’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 16 (1991), 255–310.CrossRefGoogle Scholar
Väisälä, J., ‘Free quasiconformality in Banach spaces III’, Ann. Acad. Sci. Fenn., Ser. A I, Math. 17 (1992), 393–408.Google Scholar
Väisälä, J., ‘Relatively and inner uniform domains’, Conform. Geom. Dyn. 2 (1998), 56–88.CrossRefGoogle Scholar
Väisälä, J., ‘The free quasiworld: freely quasiconformal and related maps in Banach spaces’, in: Quasiconformal Geometry and Dynamics (Lublin 1996), Banach Center Publications, 48 (Polish Academy of Science, Warsaw, 1999), 55–118.Google Scholar
Väisälä, J., ‘Broken tubes in Hilbert spaces’, Analysis 24 (2004), 227–238.Google Scholar
Vuorinen, M., Conformal Geometry and Quasiregular Mappings, Lecture Notes in Mathematics, 1319 (Springer, Berlin, 1988).Google Scholar