Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T22:43:22.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractional integrals of generalised functions

Published online by Cambridge University Press:  09 April 2009

A. Erdélyi
A. Erdélyi
Affiliation:
University of Edinburgh and University of Melbourne
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

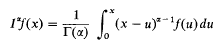The concept of integrals of fractional order of a function f, defined by if Reα > 0, can be extended to generalised functions in the framework of the theory of convolution of distributions. The resulting theory [2, Chap. I §5.5] is very satisfactory for many purposes but there are circumstances in which it is not suitable. Such circumstances arise in particular if it is necessary to multiply, before or after integratrion, by non-integral powers of the variable. Pointwise multiplication by fractional powers of the independent variable does not make sense in the theory of distributions.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 14 , Issue 1 , July 1972 , pp. 30 - 37
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Erdèlyi, A. and McBride, A. C. ‘Fractional integrals of distributions’, SIAM J. on Math. Analysis (1970) 547–557.CrossRefGoogle Scholar
[2]Gelfand, I. M. and Shilov, G. E., Generalized functions Vol. 1 (Academic Press, New York, 1964).Google Scholar
[3]Kober, H., ‘On fractional integrals and derivatives’, Quart. J. of Math. (Oxford) 11 (1940), 193–211.Google Scholar
[4]Love, E. R., ‘Some integral equations involving hypergeometric functions’, Proc. Edinburgh Math. Soc. (2) 15 (1967), 169–198.Google Scholar
[5]Love, E. R., ‘Two more hypergeometric integral equations’, Proc. Cambridge Philos. Soc. 63 (1967), 1055–1076.CrossRefGoogle Scholar
[6]Love, E. R., ‘Two index laws for fractional integrals and derivatives’, to appear in the J. of Australian Math. Soc.Google Scholar
[7]Love, E. R. and Young, L. C., ‘On fractional integration by parts’, Proc. London Math. Soc. (2) 44 (1938), 1–28.CrossRefGoogle Scholar
[8]Zemanian, A. H., Generalized integral transformations (Interscience Publishers, New York, 1968).Google Scholar