Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T12:36:05.154Z Has data issue: false hasContentIssue false
  • English
  • Français

Fonctions propres de l'opérateur de Laplace-Beltrami associé au bi-disque

Part of: General; Abstract harmonic analysis Abstract harmonic analysis

Published online by Cambridge University Press:  09 April 2009

Taoufiq Tahani
Taoufiq Tahani
Affiliation:
Université des Sciences et Techniques deLille Flandres-Artois U.F.R. de Mathématiques Pures et Appliquées 59650 Villeneuve d'ascq, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit D I'opérateur de Laplace-Beltrami sur le bi-disque. On démontre que les fonctions ζ → Plgr; (ζ, u) provenant du noyau de Poisson associé au bi-disque sont les seules solutions réelles normalisées du système. 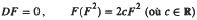qui satisfont une certaine hypothèse.

MSC classification

Secondary: 43-02: Research exposition (monographs, survey articles) 43A75: Analysis on specific compact groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 53 , Issue 2 , October 1992 , pp. 183 - 197
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Chipot, M., Eymard, P. and Tahani, T., ‘Sur les fonctions propres de l'opérateur de Laplace-Beltrami dont le carré est fonction propre’, Symposia Mathematica 29 (1988), 111–129.Google Scholar
[2]Chipot, M. and Oliker, V., ‘Sur une propriété des fonctions propres de l'opérateur de Laplace-Beltrami’, preprint.Google Scholar
[3]Eymard, P., ‘Le Noyau de Poission et l'Analyse Harmonique non Euclidienne’, Topics in modern harmonic analysis, (Ist. Nazionale di Alta Matematica, Roma, 1983).Google Scholar
[4]Kawazoe, T., ‘A property of the eigenfunctions of the Laplace-Beltrami operator on the classical real rank one symmetric spaces’, preprint.Google Scholar
[5]Kawazoe, T. and Tahani, T., ‘A characterization of the Poission kernel associated with SU(1, n)’, Tokyo J. Math. 11, No. 1 (1988), 37–55.CrossRefGoogle Scholar
[6]Korányi, A., A survey of harmonic functions on symmetric spaces, (Proceedings of Symposia in Pure Mathematics, Volume 35, Part 1, 1979).Google Scholar
[7]Rudin, W., Function theory in the unit ball of Cn, (Springer-Verlag, 1980).CrossRefGoogle Scholar
[8]Tahani, T., Fonctions propres de l'opérateur de Laplace-Beltrami dans les boules hyporboliques réelles ou complexes, thèse de 3ème cycle, Université de Nancy I (1985).Google Scholar