Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tarafdar, E.
1976.
On a fixed-point theorem on locally convex linear topological spaces.
Monatshefte f�r Mathematik,
Vol. 82,
Issue. 4,
p.
341.
Wong, Chi Song
1976.
Approximation to fixed points of generalized nonexpansive mappings.
Proceedings of the American Mathematical Society,
Vol. 54,
Issue. 1,
p.
93.
Staples, John
1976.
Asymptotic centres of filters on uniformly rotund spaces.
Bulletin of the Australian Mathematical Society,
Vol. 15,
Issue. 1,
p.
87.
Ivanov, A. A.
1979.
Fixed points of mappings of metric spaces.
Journal of Soviet Mathematics,
Vol. 12,
Issue. 1,
p.
1.
Chen, Ming-Po
and
Shih, Mau-Hsiang
1979.
Fixed point theorems for point-to-point and point-to-set maps.
Journal of Mathematical Analysis and Applications,
Vol. 71,
Issue. 2,
p.
516.
Fisher, B.
and
Sessa, S.
1986.
Nonlinear Functional Analysis and Its Applications.
p.
223.
Betiuk-Pilarska, A.
and
Domínguez Benavides, T.
2015.
The fixed point property for some generalized nonexpansive mappings and renormings.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
800.
Fukhar-ud-din, Hafiz
and
Saleh, Khairul
2016.
One-Step Iterations for a Finite Family of Generalized Nonexpansive Mappings in CAT(0) Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,


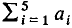 < 1 and for any
< 1 and for any