Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:26:48.940Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE FIELD EXTENSIONS WITH THE LINE OR TRANSLATE PROPERTY FOR $r$-PRIMITIVE ELEMENTS

Part of: Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  02 March 2020

STEPHEN D. COHEN Open the ORCID record for STEPHEN D. COHEN [Opens in a new window]  and
GIORGOS KAPETANAKIS Open the ORCID record for GIORGOS KAPETANAKIS [Opens in a new window]
STEPHEN D. COHEN
Affiliation:
6 Bracken Road, Portlethen, AberdeenAB12 4TA, UK e-mail: [email protected]
GIORGOS KAPETANAKIS*
Affiliation:
Department of Mathematics and Applied Mathematics, University of Crete, Voutes Campus, 70013Heraklion, Greece
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 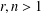$r,n>1$ be integers and 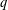$q$ be any prime power 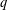$q$ such that 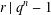$r\mid q^{n}-1$. We say that the extension 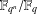$\mathbb{F}_{q^{n}}/\mathbb{F}_{q}$ possesses the line property for $r$-primitive elements property if, for every 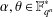$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703}\in \mathbb{F}_{q^{n}}^{\ast }$ such that 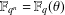$\mathbb{F}_{q^{n}}=\mathbb{F}_{q}(\unicode[STIX]{x1D703})$, there exists some 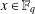$x\in \mathbb{F}_{q}$ such that 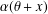$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}+x)$ has multiplicative order 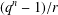$(q^{n}-1)/r$. We prove that, for sufficiently large prime powers 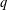$q$, 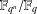$\mathbb{F}_{q^{n}}/\mathbb{F}_{q}$ possesses the line property for $r$-primitive elements. We also discuss the (weaker) translate property for extensions.

Keywords

primitive elementhigh-order elementline propertytranslate property

MSC classification

Primary: 11T30: Structure theory
Secondary: 11T06: Polynomials
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 3 , December 2021 , pp. 313 - 319
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

Communicated by I. Shparlinski

The first author is Emeritus Professor of Number Theory, University of Glasgow.

References

Apostol, T. M., Introduction to Analytic Number Theory (Springer, New York, 1976).Google Scholar
Bailey, G., Cohen, S. D., Sutherland, N. and Trudgian, T., ‘Existence results for primitive elements in cubic and quartic extensions of a finite field’, Math. Comp. 88(316) (2019), 931–947.10.1090/mcom/3357CrossRefGoogle Scholar
Carlitz, L., ‘Distribution of primitive roots in a finite field’, Quart. J. Math. Oxford Ser. (2) 4(1) (1953), 4–10.10.1093/qmath/4.1.4CrossRefGoogle Scholar
Cohen, S. D., ‘Primitive roots in the quadratic extension of a finite field’, J. Lond. Math. Soc. (2) 27(2) (1983), 221–228.10.1112/jlms/s2-27.2.221CrossRefGoogle Scholar
Cohen, S. D., ‘Generators of the cubic extension of a finite field’, J. Comb. Number Theory 1(3) (2009), 189–202.Google Scholar
Cohen, S. D., ‘Primitive elements on lines in extensions of finite fields’, in: Finite Fields: Theory and Applications, Contemporary Mathematics, 518 (eds. McGuire, G., Mullen, G. L., Panario, D. and Shparlinski, I. E.) (American Mathematical Society, Province, RI, 2010), 113–127.10.1090/conm/518/10200CrossRefGoogle Scholar
Cohen, S. D. and Kapetanakis, G., ‘The trace of 2-primitive elements of finite fields’, Acta Arith. 192(4) (2020), 397–419.10.4064/aa190307-23-5CrossRefGoogle Scholar
Davenport, H., ‘On primitive roots in finite fields’, Quart. J. Math. Oxford 8(1) (1937), 308–312.10.1093/qmath/os-8.1.308CrossRefGoogle Scholar
Gao, S., ‘Elements of provable high orders in finite fields’, Proc. Amer. Math. Soc. 127(6) (1999), 1615–1623.10.1090/S0002-9939-99-04795-4CrossRefGoogle Scholar
Huczynska, S., Mullen, G. L., Panario, D. and Thomson, D., ‘Existence and properties of k-normal elements over finite fields’, Finite Fields Appl. 24 (2013), 170–183.10.1016/j.ffa.2013.07.004CrossRefGoogle Scholar
Kapetanakis, G. and Lavrauw, M., ‘A geometric condition for primitive semifields’, 2019, in preparation.Google Scholar
Kapetanakis, G. and Reis, L., ‘Variations of the primitive normal basis theorem’, Des. Codes Cryptogr. 87(7) (2019), 1459–1480.10.1007/s10623-018-0543-9CrossRefGoogle Scholar
Katz, N. M., ‘An estimate for character sums’, J. Amer. Math. Soc. 2(2) (1989), 197–200.10.1090/S0894-0347-1989-0965007-8CrossRefGoogle Scholar
Martínez, F. E. B. and Reis, L., ‘Elements of high order in Artin-Schreier extensions of finite fields 𝔽q ’, Finite Fields Appl. 41 (2016), 24–33.10.1016/j.ffa.2016.05.002CrossRefGoogle Scholar
Popovych, R., ‘Elements of high order in finite fields of the form F q[x]/(x m - a)’, Finite Fields Appl. 19(1) (2013), 92–96.10.1016/j.ffa.2012.10.006CrossRefGoogle Scholar
Rúa, I. F., ‘On the primitivity of four-dimensional finite semifields’, Finite Fields Appl. 33 (2015), 212–229.10.1016/j.ffa.2014.12.009CrossRefGoogle Scholar
Rúa, I. F., ‘Primitive semifields of order 24e ’, Des. Codes Cryptogr. 83(2) (2017), 345–356.10.1007/s10623-016-0231-6CrossRefGoogle Scholar
Weil, A., Sur les courbes algébriques et les variétés qui s’en déduisent (Hermann, Paris, 1948).Google Scholar