Article contents
FACTORIZING MULTILINEAR KERNEL OPERATORS THROUGH SPACES OF VECTOR MEASURES
Published online by Cambridge University Press: 13 January 2020
Abstract
We consider a multilinear kernel operator between Banach function spaces over finite measures and suitable order continuity properties, namely 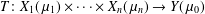 $T:X_{1}(\,\unicode[STIX]{x1D707}_{1})\times \cdots \times X_{n}(\,\unicode[STIX]{x1D707}_{n})\rightarrow Y(\,\unicode[STIX]{x1D707}_{0})$. Then we define, via duality, a class of linear operators associated to the
$T:X_{1}(\,\unicode[STIX]{x1D707}_{1})\times \cdots \times X_{n}(\,\unicode[STIX]{x1D707}_{n})\rightarrow Y(\,\unicode[STIX]{x1D707}_{0})$. Then we define, via duality, a class of linear operators associated to the 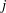 $j$-transpose operators. We show that, under certain conditions of
$j$-transpose operators. We show that, under certain conditions of 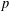 $p$th power factorability of such operators, there exist vector measures
$p$th power factorability of such operators, there exist vector measures 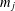 $m_{j}$ for
$m_{j}$ for  $j=0,1,\ldots ,n$ so that
$j=0,1,\ldots ,n$ so that 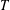 $T$ factors through a multilinear operator
$T$ factors through a multilinear operator 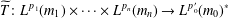 $\widetilde{T}:L^{p_{1}}(m_{1})\times \cdots \times L^{p_{n}}(m_{n})\rightarrow L^{p_{0}^{\prime }}(m_{0})^{\ast }$, provided that
$\widetilde{T}:L^{p_{1}}(m_{1})\times \cdots \times L^{p_{n}}(m_{n})\rightarrow L^{p_{0}^{\prime }}(m_{0})^{\ast }$, provided that 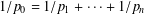 $1/p_{0}=1/p_{1}+\cdots +1/p_{n}$. We apply this scheme to the study of the class of multilinear Calderón–Zygmund operators and provide some concrete examples for the homogeneous polynomial and multilinear Volterra and Laplace operators.
$1/p_{0}=1/p_{1}+\cdots +1/p_{n}$. We apply this scheme to the study of the class of multilinear Calderón–Zygmund operators and provide some concrete examples for the homogeneous polynomial and multilinear Volterra and Laplace operators.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by C. Meaney
References
- 1
- Cited by



