Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T09:17:49.355Z Has data issue: false hasContentIssue false
  • English
  • Français

FACTORISATION OF EQUIVARIANT SPECTRAL TRIPLES IN UNBOUNDED 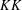$KK$-THEORY

Part of: Selfadjoint operator algebras $K$-theory and operator algebras

Published online by Cambridge University Press:  21 December 2018

IAIN FORSYTH  and
ADAM RENNIE
IAIN FORSYTH
Affiliation:
Mathematical Sciences Institute, Australian National University, Canberra, Australia School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, Australia Institut für Analysis, Leibniz Universität Hannover, Germany email [email protected]
ADAM RENNIE*
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide sufficient conditions to factorise an equivariant spectral triple as a Kasparov product of unbounded classes constructed from the group action on the algebra and from the fixed point spectral triple. We show that if factorisation occurs, then the equivariant index of the spectral triple vanishes. Our results are for the action of compact abelian Lie groups, and we demonstrate them with examples from manifolds and 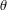$\unicode[STIX]{x1D703}$-deformations. In particular, we show that equivariant Dirac-type spectral triples on the total space of a torus principal bundle always factorise. Combining this with our index result yields a special case of the Atiyah–Hirzebruch theorem. We also present an example that shows what goes wrong in the absence of our sufficient conditions (and how we get around it for this example).

Keywords

KK-theoryspectral tripleKasparov product

MSC classification

Primary: 19K35: Kasparov theory ($KK$-theory)
Secondary: 46L87: Noncommutative differential geometry
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 145 - 180
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Atiyah, M. and Hirzebruch, F., ‘Spin-manifolds and group actions’, in: Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham) (Springer, Berlin, 1970), 18–28.Google Scholar
Baaj, S. and Julg, P., ‘Théorie bivariante de Kasparov et opérateurs non bornées dans les C ∗ -modules hilbertiens’, C. R. Acad. Sci. Paris 296 (1983), 875–878.Google Scholar
Berline, N., Getzler, E. and Vergne, M., Heat Kernels and Dirac Operators (Springer, Berlin, 2004).Google Scholar
Brain, S., Mesland, B. and van Suijlekom, W. D., ‘Gauge theory for spectral triples and the unbounded Kasparov product’, J. Noncommut. Geom. 10(1) (2016), 135–206.Google Scholar
Carey, A. L., Gayral, V., Rennie, A. and Sukochev, F. A., ‘Index theory for locally compact noncommutative geometries’, Mem. Amer. Math. Soc. 231(1085) (2014).Google Scholar
Carey, A. L., Neshveyev, S., Nest, R. and Rennie, A., ‘Twisted cyclic theory, equivariant KK-theory and KMS states’, J. reine angew. Math. 650 (2011), 161–191.Google Scholar
Chamseddine, A., Connes, A. and van Suijlekom, W., ‘Inner fluctuations in noncommutative geometry without the first order condition’, J. Geom. Phys. 73 (2013), 222–234.Google Scholar
Connes, A., Noncommutative Geometry (Academic Press, San Diego, CA, 1994).Google Scholar
Connes, A. and Landi, G., ‘Noncommutative manifolds: the instanton algebra and isospectral deformations’, Commun. Math. Phys. 221 (2001), 141–159.Google Scholar
Dabrowski, L. and Sitarz, A., ‘Noncommutative circle bundles and new Dirac operators’, Commun. Math. Phys. 318 (2013), 111–130.Google Scholar
Dabrowski, L., Sitarz, A. and Zucca, A., ‘Dirac operators on noncommutative principal circle bundles’, Int. J. Geom. Methods Mod. Phys. 11 (2014).Google Scholar
Gracia-Bondía, J. M., Várilly, J. C. and Figueroa, H., Elements of Noncommutative Geometry (Birkhäuser, Boston, 2001).Google Scholar
Higson, N. and Roe, J., Analytic K-Homology (Oxford University Press, Oxford, 2000).Google Scholar
Kaad, J. and Lesch, M., ‘Spectral flow and the unbounded Kasparov product’, Adv. Math. 248 (2013), 495–530.Google Scholar
Kasparov, G. G., ‘The operator K-functor and extensions of C ∗ -algebras’, Math. USSR Izv. 16 (1981), 513–572.Google Scholar
Kucerovsky, D., ‘The KK-product of unbounded modules’, J. K-Theory 11 (1997), 17–34.Google Scholar
Kucerovsky, D., ‘A lifting theorem giving an isomorphism of KK-products in bounded and unbounded KK-theory’, J. Operator Theory 44 (2000), 255–275.Google Scholar
Lance, E. C., Hilbert C ∗ -Modules (Cambridge University Press, Cambridge, 1995).Google Scholar
Lawson, H. B. and Michelsohn, M.-L., Spin Geometry (Princeton University Press, Princeton, NJ, 1989).Google Scholar
Mesland, B., ‘Unbounded bivariant K-theory and correspondences in noncommutative geometry’, J. Reine Angew. Math. 691 (2014), 101–172.Google Scholar
Mesland, B. and Rennie, A., ‘Nonunital spectral triples and metric completeness in unbounded KK-theory’, J. Funct. Anal. 271(9) (2016), 2460–2538.Google Scholar
Pask, D. and Rennie, A., ‘The noncommutative geometry of graph C ∗ -algebras I: the index theorem’, J. Funct. Anal. 233 (2006), 92–134.Google Scholar
Phillips, N. C., Equivariant K-Theory and Freeness of Group Actions on C ∗ -Algebras (Springer, Berlin, 1987).Google Scholar
Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-Trace C ∗ -algebras (American Mathematical Society, Providence, RI, 1998).Google Scholar
Reinhart, B. L., ‘Foliated manifolds with bundle-like metrics’, Ann. of Math. (2) 69 (1959), 119–132.Google Scholar
Rieffel, M. A., ‘Deformation quantization for actions of ℝ d ’, Mem. Amer. Math. Soc. 106(506) (1993).Google Scholar
Schwieger, K. and Wagner, S., ‘Free actions of compact groups on C ∗ -algebras, part I’, Adv. Math. 317 (2017), 224–266.Google Scholar
Slebarski, S., ‘Dirac operators on a compact Lie group’, Bull. Lond. Math. Soc. 17 (1985), 579–583.Google Scholar
Várilly, J. C., An Introduction to Noncommutative Geometry (European Mathematical Society, Zurich, 2006).Google Scholar
Zucca, A., Dirac Operators on Quantum Principal G-Bundles (Digital Library, Scuola Internazionale Superiore di Studi Avanzati, Trieste, 2013).Google Scholar