Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T09:00:36.318Z Has data issue: false hasContentIssue false
  • English
  • Français

EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO

Part of: Representation theory of rings and algebras Basic linear algebra Homological methods

Published online by Cambridge University Press:  19 September 2016

KARIN ERDMANN
KARIN ERDMANN*
Affiliation:
Mathematical Institute, University of Oxford, ROQ, Oxford OX2 6GG, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that 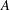$A$ is a finite-dimensional algebra over some field, and assume that 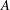$A$ is weakly symmetric and indecomposable, with radical cube zero and radical square nonzero. We show that such an algebra of wild representation type does not have a nonprojective module 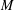$M$ whose ext-algebra is finite dimensional. This gives a complete classification of weakly symmetric indecomposable algebras which have a nonprojective module whose ext-algebra is finite dimensional. This shows in particular that existence of ext-finite nonprojective modules is not equivalent with the failure of the finite generation condition (Fg), which ensures that modules have support varieties.

Keywords

extensionsfinite global dimensionweakly symmetric algebrasChebyshev polynomials

MSC classification

Primary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 16G10: Representations of Artinian rings
Secondary: 16E05: Syzygies, resolutions, complexes 15A24: Matrix equations and identities 33C45: Orthogonal polynomials and functions of hypergeometric type (Jacobi, Laguerre, Hermite, Askey scheme, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 1 , February 2017 , pp. 108 - 121
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Assem, I., Simson, D. and Skowroński, A., ‘Elements of the representation theory of associative algebras’, in: Techniques of Representation Theory, London Mathematical Society Student Texts, 65, Vol. 1 (Cambridge University Press, Cambridge, 2006).Google Scholar
Auslander, M. and Reiten, I., ‘On a generalized version of the Nakayama conjecture’, Proc. Amer. Math. Soc. 52 (1975), 69–74.Google Scholar
Auslander, M., Reiten, I. and Smalø, S., ‘Representation theory of Artin algebras’, Cambridge Stud. Adv. Math. 36 (1995).Google Scholar
Benson, D. J., Representations and Cohomology. II. Cohomology of Groups and Modules, Cambridge Studies in Advanced Mathematics, 31 (Cambridge University Press, Cambridge, 1991).Google Scholar
Benson, D. J., ‘Resolutions over symmetric algebras with radical cube zero’, J. Algebra 320(1) (2008), 48–56.Google Scholar
Celikbas, O. and Takahashi, R., ‘Auslander–Reiten conjecture and Auslander–Reiten duality’, J. Algebra 382 (2013), 100–114.Google Scholar
Christensen, L. W. and Holm, H., ‘Algebras that satisfy Auslander’s condition on vanishing of cohomology’, Math. Z. 265 (2010), 21–40.Google Scholar
Diveris, K. and Purin, M., ‘The generalized Auslander–Reiten condition for the bounded derived category’, Arch. Math. 98(6) (2012), 507–511.Google Scholar
Diveris, K. and Purin, M., ‘Vanishing of self-extensions over symmetric algebras’, J. Pure Appl. Algebra 218(5) (2014), 962–971.Google Scholar
Erdmann, K., Holloway, M., Snashall, N., Solberg, O. and Taillefer, R., ‘Support varieties for selfinjective algebras’, K-Theory 33(1) (2004), 67–87.Google Scholar
Erdmann, K. and Schroll, S., ‘Chebyshev polynomials on symmetric matrices’, Linear Algebra Appl. 434(12) (2011), 2475–2496.Google Scholar
Erdmann, K. and Solberg, Ø., ‘Radical cube zero weakly symmetric algebras and support varieties’, J. Pure Appl. Algebra 215(2) (2011), 185–200.Google Scholar
Jorgensen, D. A., ‘Finite projective dimension and the vanishing of Ext R (M, M)’, Comm. Algebra 36(12) (2008), 4461–4471.CrossRefGoogle Scholar
Rivlin, T. J., Chebyshev Polynomials: From Approximation Theory to Algebra and Number Theory, 2nd edn, Pure and Applied Mathematics (John Wiley, New York, 1990).Google Scholar
Schulz, R., ‘Boundedness and periodicity of modules over QF rings’, J. Algebra 101 (1986), 450–469.CrossRefGoogle Scholar
Solberg, Ø., ‘Support varieties for modules and complexes’, in: Trends in Representation Theory of Algebras and Related Topics, Contemporary Mathematics, 406 (American Mathematical Society, Providence, RI, 2006), 239–270.Google Scholar