Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T08:37:41.396Z Has data issue: false hasContentIssue false
  • English
  • Français

The existence of parametric surface integrals

Published online by Cambridge University Press:  09 April 2009

J. H. Michael
J. H. Michael
Affiliation:
University of Adelaide, South Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [2] we studied parametric n-surfaces (f, Mn), where Mn was a compact, oriented, topological n-manifold and f a continuous mapping of Mn into the real euclidean k-space Rn (k≧n). A definition of bounded variation was given and, for each surface with bounded variation and each projection P from Rk to Rn, a signed measure: 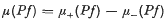Was constructed. This measure was used to define a linear type of surface integral: 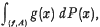over a “measurable” subset A of Mn, as the Lebesgue-Stieltjes integral: .

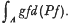Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 1 , Issue 4 , December 1960 , pp. 419 - 427
Copyright
Copyright © Australian Mathematical Society 1960

References

[1] Cesari, L., Surface Area, Annals of Mathematics Studies, 35 (1956).Google Scholar
[2] Michael, J. H., Integration over Parametric Surfaces, Proc. Lond. Math. Soc., Ser. 3, 7 (1957), 616–640.CrossRefGoogle Scholar
[3] Whyburn, G. T., Analytic Topology, American Math. Soc. Colloquium Publications, 28.Google Scholar