Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T06:48:16.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Essentially commutative C*-algebras with essential spectrum homeomorphic to S2n−1

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  09 April 2009

Kunyu Guo
Kunyu Guo
Affiliation:
Department of Mathematics Fudan UniversityShanghai, 200433 P.R.China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper gives a complete classification of essentially commutative C*-algebras whose essential spectrum is homeomorphic to S2n−1 by their characteristic numbers. Let 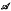1, 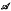2 be such two C*-algebras; then they are C*-isomorphic if and only if they have the same n-th characteristic number. Furthermore, let γn(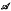) = m then 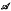is C*-isomorphic to C*(Mzl, …, Mzn) if m = 0, 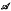is C*-isomorphic C*(Tz1, …, Tzn−1, Tznm) if m ≠ 0. Some examples are given to show applications of the classfication theorem. We finally remark that the proof of the theorem depends on a construction of a complete system of representatives of Ext(S2n−1).

Keywords

characteristic numbersessential spectrumextensionsmapping degree.

MSC classification

Secondary: 47A53: (Semi-) Fredholm operators; index theories 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators 47B37: Operators on special spaces (weighted shifts, operators on sequence spaces, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 70 , Issue 2 , April 2001 , pp. 199 - 210
Copyright
Copyright © Australian Mathematical Society 2001

References

[Ati]Atiyah, M. F., ‘Algebra topology and elliptic operators’, Comm. Pure Appl. Math. 20 (1967), 237–249.CrossRefGoogle Scholar
[Bla]Blackadar, B., K-Theory for operator algebras (Springer, New York, 1986).CrossRefGoogle Scholar
[BT]Bott, R. and Tu, L. W., Differential forms in algebraic topology (Springer, New York, 1982).CrossRefGoogle Scholar
[BDF1]Brown, L. G., Douglas, R. G. and Fillmore, P. A., Unitary equivalence modulo the compact operators and extensions of C*-algebras, Lecture Notes in Math. 345 (Springer, Berlin, 1973).CrossRefGoogle Scholar
[BDF2]Brown, L. G., Douglas, R. G. and Fillmore, P. A., ‘Extensions of C*-algebras and K-homology’, Ann. of Math. (2) 105 (1977), 265–324.CrossRefGoogle Scholar
[Cob]Coburn, L. A., ‘Singular integral operators and Toeplitz operators on odd sphere’, Indiana Univ. Math. J. 23 (1973), 433–439.CrossRefGoogle Scholar
[Cur]Curto, R. E., ‘Fredholm and invertible n-tuples of operators. The deformation problem’, Trans. Amer. Math. Soc. 266 (1981), 129–159.Google Scholar
[CS]Curto, R. E. and Salinas, N., ‘Spectral properties of cyclic subnormal m-tuples’, Amer. J. Math. 107 (1985), 113–138.CrossRefGoogle Scholar
[Dou]Douglas, R. G., Banach algebra techniques in operator theory (Academic Press, New York, 1972).Google Scholar
[Fre]Freedman, M., ‘The topology of 4-manifold’, J. Differential Geom. 17 (1982), 357–454.CrossRefGoogle Scholar
[Guo1]Guo, K. Y., ‘Indices, characteristic numbers and essential commutants of Toeplitz operators’, Ark. Mat. 38 (2000), 97–110.CrossRefGoogle Scholar
[Guo2]Guo, K. Y., ‘Indices, of Toeplitz tuples on pseudoregular domains’, Science in China 43 (2000), 1258–1268.Google Scholar
[Hir]Hirsch, M. W., Differential topology (Springer, New York, 1976).Google Scholar
[Sal]Salinas, N., ‘The -formalism and the C*-algebras of the Bergman n-tuple’, J. Operator Theory 22 (1989), 325–343.Google Scholar
[SSU]Salinas, N., Sheu, A. and Upmeier, H., ‘Toeplitz operators on pseudoconvex domains and foliation C*-algebras’, Ann. of Math. (2) 130 (1989), 531–565.Google Scholar
[Sma1]Smale, S., ‘A Survey of some recent developments in differential topology’, Bull. Amer. Math. Soc. 69 (1963), 131–146.Google Scholar
[Sma2]Smale, S., ‘Generalized Poincaré conjecture in dimensional greater than four’, Ann. of Math. (2) 74 (1961), 391–406.CrossRefGoogle Scholar
[Ven]Venugopalkrishna, U., ‘Fredholm operators associated with strongly pseudoconvex domains in Cn’, J. Funct. Anal. 9 (1972), 349–372.CrossRefGoogle Scholar