Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sharifi, Kamran
2017.
Atiyah-Jänich Theorem for σ-C*-algebras.
Applied Categorical Structures,
Vol. 25,
Issue. 5,
p.
893.


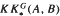 are extended to the setting of inverse limits of
are extended to the setting of inverse limits of 