Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:13:43.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Enlarging the Munn representation of inverse semigroups

Published online by Cambridge University Press:  09 April 2009

N. R. Reilly
N. R. Reilly
Affiliation:
Simon Fraser University, Burnaby V5A 1S6, British Columbia, Canada.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The inverse semigroup TE of isomorphisms of principal ideals of E onto principal ideals of E, where E is a semilattice, has been introduced and studied by Munn (1966, 1970). He showed that, for any inverse semigroup S with semilattice E, there is a representation of S by an inverse subsemigroup of TE. The Munn representation, however, is not always faithful. In this paper, the possibility is considered of enlarging the carrier set E of the Munn representation in order to obtain a faithful representation of S as an inverse subsemigroup of a structure resembling TE in many ways. A structure X is obtained by replacing each element of E by a set. Then X = ∪{Xe: e ∈ E}, where Xe, denotes some set, has a natural pre-order relation ≤ (where x ≤ y if and only if x ∈ Xe, y ∈ Xf and e ≦ f ) inherited from E such that if T = {(x, y)∈X × X;x ≤ y and y ≤ x} then X/T is isomorphic to E. Such a set X is referred to as a pre-semilattice with semilattice E. If Tx denotes the set of all isomorphisms of principal ideals of X onto principal ideals of X then Tx is an inverse semigroup. Basic properties of Tx are considered. It is shown that when X is locally uniform, that is, when |Xe| = |Xf|, for all e, f ∈ E, Tx may be described as a wreath product of a permutation group with TE.

The set s itself is a presemilattice with semilattice E with respect to the pre-order ≤ defined by a ≤ b if and only if a−1a ≦ b−1b. It is then shown that the Vagner-Preston representation embeds S as a full inverse subsemigroup of Ts. As an application of these concepts the following result is established. Let R and S be inverse semigroups and let θ1(θ2) be an isomorphism of a semilattice E onto the semilattice of R(S). Then there exists a locally uniform presemilattice W and embeddings ϕ1, ϕ2 of R and S, respectively, as full inverse subsemigroups of Tw such that (1) θ1ϕ1 = θ2ϕ2 and (2) (eθ1ϕ1, eθ2ϕ2) ∈ 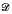if and only if Ee is isomorphic to Ef.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 23 , Issue 1 , February 1977 , pp. 28 - 41
Copyright
Copyright © Australian Mathematical Society 1977

References

Clifford, A. H. and Preston, G. B. (1961), The algebraic theory of semigroups, Math. Surveys of the American Math. Soc. 7 (Providence, R.I. 1961 (Vol. 1)).Google Scholar
Clifford, A. H. and Preston, G. B. (1967), The algebraic theory of semigroups, Math. Surveys of the American Math. Soc. 7 (Providence R.I. 1967 (Vol. 2)).Google Scholar
Hall, T. E. (1975), ‘Free products with amalgamation of inverse semigroups’, J. Algebra 34, 375–385.CrossRefGoogle Scholar
Howie, J. M. (1964), ‘The maximum idempotent separating congruence on an inverse semigroup’, Proc. Edinburgh Math. Soc. (2) 14, 71–79.CrossRefGoogle Scholar
Howie, J. M. (1975), ‘Semigroup amalgams whose cores are inverse semigroups’, Quart. J. Math. Oxford (2) 26, 23–45.CrossRefGoogle Scholar
Munn, W. D. (1966), ‘Uniform semilattices and bisimple inverse semigroups’, Quart. J. Math. Oxford (2), 17, 151–159.CrossRefGoogle Scholar
Munn, W. D. (1970), ‘Fundamental inverse semigroups’, Quart. J. Math. Oxford (2), 21, 157–170.CrossRefGoogle Scholar