Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T05:14:47.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Engel Series Expansions of Laurent Series and Hausdorff Dimensions

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  09 April 2009

Jun Wu
Jun Wu
Affiliation:
Department of Mathematics Wuhan UniversityWuhan, Hubei, 430072 People's Republic of China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any positive integer q≧2, let Fq be a finite field with q elements, Fq ((z-1)) be the field of all formal Laurent series 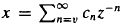in an inderminate z, I denote the valuation ideal z-1Fq [[z-1]] in the ring of formal power series Fq ((z-1)) normalized by P(l) = 1. For any x ∈ I, let the series 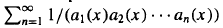be the Engel expansin of Laurent series of x. Grabner and Knopfmacher have shown that the P-measure of the set A(α) = {x ∞ I: limn→∞ deg an(x)/n = ά} is l when α = q/(q -l), where deg an(x) is the degree of polynomial an(x). In this paper, we prove that for any α ≧ l, A(α) has Hausdorff dimension l. Among other thing we also show that for any integer m, the following set B(m) = {x ∈ l: deg an+1(x) - deg an(x) = m for any n ≧ l} has Hausdorff dimension 1.

MSC classification

Secondary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 11T06: Polynomials 28A80: Fractals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 75 , Issue 1 , August 2003 , pp. 1 - 7
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Andrews, G. E., Knopfmacher, A. and Knopfmacher, J., ‘Engel expansions and the Rogers Ramanujan identities’, J. Number Theory (2) 80 (2000), 273–290.Google Scholar
[2]Andrews, G. E., Knopfmacher, A. and Paule, P., ‘An infinite family of Engel expansions of RogersRamanujan type’, Adv. Appl. Math. (1) 25 (2000), 2–11.Google Scholar
[3]Erdös, P., Rényi, A. and Szüsz, P., ‘On Engel's and Sylvester's series’, Ann. Univ. Sci. Budapest, Sectio Math. 1 (1958), 7–32.Google Scholar
[4]Falconer, K. J., Fractal geometry, mathematical foundations and applications (John Wiley, New York, 1990).Google Scholar
[5]Galambos, J., Representations of real numbers by infinite series, Lecture Notes in Math. 502 (Springer, Berlin, 1976).CrossRefGoogle Scholar
[6]Grabner, P. J. and Knopfmacher, A., ‘Metric properties of Engel series expansions of Laurent series’, Math. Slovaca (3) 48 (1998), 233–243.Google Scholar
[7]Jones, W. B. and Thron, W. J., Continued fractions (Addison-Wesley, 1980).Google Scholar
[8]Knopfmacher, A. and Knopfmacher, J., ‘Inverse polynomial expansions of Laurent series’, Constr. Approx. (4) 4 (1988), 379–389.Google Scholar
[9]Knopfmacher, A. and Knopfmacher, J., ‘Inverse polynomial expansions of Laurent series, II’, J. Comput. Appl. Math. 28 (1989), 249–257.Google Scholar
[10]Liu, Y. Y. and Wu, J., ‘Hausdorff dimensions in Engel expansions’, Acta Arith. (1) 99 (2001), 79–83.Google Scholar
[11]Renyi, A., ‘A new approach to the theory of Engel's series’, Ann. Univ. Sci. Budapest, Sectio Math. 5 (1962), 25–32.Google Scholar