Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T03:27:39.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding a semigroup of transformations

Published online by Cambridge University Press:  09 April 2009

J. S. V. Symons
J. S. V. Symons
Affiliation:
Monash UniversityClayton 3168, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be an arbitrary set and θ a transformation of X. One may use θ to induce an associative operation in Jx, the set of all mappings of X to itself as follows: 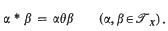. We denote the resulting semigroup by {Jx;θ) Magill (1967) introduced this structure and it has been studied by Sullivan and by myself.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 20 , Issue 2 , September 1975 , pp. 222 - 224
Copyright
Copyright © Australian Mathematical Society 1975

References

Magill, K. D. Jr, (1967), ‘Semigroup structures for familes of functions, I. Some homomorphism theorems’, J. Austral. Math. Soc. 7, 81–94.CrossRefGoogle Scholar
Sullivan, R. P. (to appear), ‘Generalized partial transformation semigroups’, J. Austral. Math. Soc.Google Scholar
Symons, J. S. V. (to appear), ‘On a generalization of the transformation semigroup’, J. Austral. Math. Soc.Google Scholar
Symons, J. S. V. (1973), Automorphisms of transformation semigroups (Ph.D. thesis, University of Western Australia, 1973).Google Scholar