Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T08:14:46.776Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of smoothness on variation

Published online by Cambridge University Press:  09 April 2009

P. G. Howlett
P. G. Howlett
Affiliation:
School of Mathematics, South Australian Institute of Technology, Adelaide, South Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be the set of real numbers, and let S1 denote the class of all real valued functions f on R which are smooth to the first order (i.e. the derivative ƒ(1) exists and is continuous) and have compact support. The first order variation off on an open set U is given by 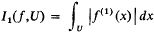and in the case where U = R we have the total first order variation of f, usually denoted by I1(f).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 1 , August 1974 , pp. 119 - 128
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Fleming, W. H. and Rishell, R., ‘An integral formula for total gradient variation’, Arch. Math. 11 (1960) 218–222.CrossRefGoogle Scholar
[2]Goffman, C., ‘Lower semi-continuity and area functionals. The non-parametric case’, Rend. Circ. Mat. Palermo (2), 2 (1953) 203–235.CrossRefGoogle Scholar
[3]Goffman, C., ‘Approximation of non-parametric surfaces of finite area’, J. Math. and Mech. 12, 5 (1963), 737–746.Google Scholar
[4]Howlett, P. G., ‘Approximation to summable functions’ (Thesis, University of Adelaide (1971) 33–148).Google Scholar
[5]Michael, J. H., ‘The equivalence of two cases for non-parametric discontinuous surfaces’, Illinois J. Math. 7 (1963), 59–78.CrossRefGoogle Scholar
[6]Michael, J. H., ‘Approximation of functions by means of Lipschitz functions’, J. Austral. Math. Soc. 3, 2 (1963), 134–150.CrossRefGoogle Scholar
[7]Michael, J. H., ‘Lipschitz approximations to summable functions’, Acta Math. 3 (1964), 73–95.CrossRefGoogle Scholar