Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T08:57:31.176Z Has data issue: false hasContentIssue false
  • English
  • Français

DUALITIES FOR MAXIMAL COACTIONS

Part of: Selfadjoint operator algebras Methods of category theory in functional analysis

Published online by Cambridge University Press:  12 May 2016

S. KALISZEWSKI ,
TRON OMLAND  and
JOHN QUIGG
S. KALISZEWSKI
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, Arizona 85287, USA email [email protected]
TRON OMLAND
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, Arizona 85287, USA email [email protected]
JOHN QUIGG*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, Arizona 85287, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a new construction of crossed-product duality for maximal coactions that uses Fischer’s work on maximalizations. Given a group 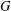$G$ and a coaction $(A,\unicode[STIX]{x1D6FF})$ we define a generalized fixed-point algebra as a certain subalgebra of 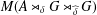$M(A\rtimes _{\unicode[STIX]{x1D6FF}}G\rtimes _{\,\widehat{\unicode[STIX]{x1D6FF}}}G)$, and recover the coaction via this double crossed product. Our goal is to formulate this duality in a category-theoretic context, and one advantage of our construction is that it breaks down into parts that are easy to handle in this regard. We first explain this for the category of nondegenerate *-homomorphisms and then, analogously, for the category of 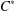$C^{\ast }$-correspondences. Also, we outline partial results for the ‘outer’ category, which has been studied previously by the authors.

Keywords

actioncoactioncrossed-product dualitycategory equivalenceC∗ -correspondenceexterior equivalenceouter conjugacy

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46M15: Categories, functors
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 2 , April 2017 , pp. 224 - 254
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The second author is funded by the Research Council of Norway (Project no. 240913).

References

Buss, A. and Echterhoff, S., ‘Universal and exotic generalized fixed-point algebras for weakly proper actions and duality’, Indiana Univ. Math. J. 63 (2014), 1659–1701.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S. and Quigg, J., ‘Maximal coactions’, Internat. J. Math. 15 (2004), 47–61.CrossRefGoogle Scholar
Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Naturality and induced representations’, Bull. Aust. Math. Soc. 61 (2000), 415–438.Google Scholar
Echterhoff, S., Kaliszewski, S., Quigg, J. and Raeburn, I., A categorical approach to imprimitivity theorems for C ∗ -dynamical systems, Memoirs of the American Mathematical Society, 180 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Fischer, R., ‘Maximal coactions of quantum groups’, Preprint no. 350, SFB 478 Geometrische Strukturen in der Mathematik, WWU Münster, 2004.Google Scholar
an Huef, A., Kaliszewski, S., Raeburn, I. and Williams, D. P., ‘Naturality of Rieffel’s Morita equivalence for proper actions’, Algebr. Represent. Theory 14 (2011), 515–543.Google Scholar
an Huef, A., Quigg, J., Raeburn, I. and Williams, D. P., ‘Full and reduced coactions of locally compact groups on C ∗ -algebras’, Expo. Math. 29 (2011), 3–23.CrossRefGoogle Scholar
Imai, S. and Takai, H., ‘On a duality for C ∗ -crossed products by a locally compact group’, J. Math. Soc. Japan 30 (1978), 495–504.CrossRefGoogle Scholar
Kaliszewski, S., Omland, T. and Quigg, J., ‘Destabilization’, Expo. Math. 34 (2016), 62–81.CrossRefGoogle Scholar
Kaliszewski, S., Omland, T. and Quigg, J., ‘Three versions of categorical crossed-product duality’, New York J. Math., 22 (2016), 293–339.Google Scholar
Kaliszewski, S. and Quigg, J., ‘Landstad’s characterization for full crossed products’, New York J. Math. 13 (2007), 1–10.Google Scholar
Kaliszewski, S. and Quigg, J., ‘Categorical Landstad duality for actions’, Indiana Univ. Math. J. 58 (2009), 415–441.CrossRefGoogle Scholar
Kaliszewski, S., Quigg, J. and Raeburn, I., ‘Proper actions, fixed-point algebras and naturality in nonabelian duality’, J. Funct. Anal. 254 (2008), 2949–2968.CrossRefGoogle Scholar
Katayama, Y., ‘Takesaki’s duality for a non-degenerate co-action’, Math. Scand. 55 (1984), 141–151.CrossRefGoogle Scholar
Lance, E. C., Hilbert C ∗ -modules, London Mathematical Society Lecture Note Series, 210 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Landstad, M. B., ‘Duality theory for covariant systems’, Trans. Amer. Math. Soc. 248 (1979), 223–267.Google Scholar
Landstad, M. B., Phillips, J., Raeburn, I. and Sutherland, C. E., ‘Representations of crossed products by coactions and principal bundles’, Trans. Amer. Math. Soc. 299 (1987), 747–784.Google Scholar
Pedersen, G. K., ‘Dynamical systems and crossed products’, in: Operator Algebras and Applications, Part I, Kingston, Ont., 1980, Proc. Sympos. Pure Math., 38 (American Mathematical Society, Providence, RI, 1982), 271–283.Google Scholar
Quigg, J., ‘Landstad duality for C ∗ -coactions’, Math. Scand. 71 (1992), 277–294.Google Scholar
Quigg, J., ‘Full and reduced C ∗ -coactions’, Math. Proc. Cambridge Philos. Soc. 116 (1994), 435–450.CrossRefGoogle Scholar
Quigg, J. and Raeburn, I., ‘Induced C ∗ -algebras and Landstad duality for twisted coactions’, Trans. Amer. Math. Soc. 347 (1995), 2885–2915.Google Scholar