Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:19:45.849Z Has data issue: false hasContentIssue false
  • English
  • Français

A Dirichlet series expansion for the p-adic zeta-function

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 April 2009

Daniel Delbourgo
Daniel Delbourgo
Affiliation:
Department of Mathematics, University Park, Nottingham, England, NG7 2RD, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

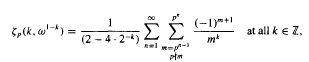We prove that the p-adic zeta-function constructed by Kubota and Leopoldt has the Dirichlet series expansion Where the convergence of the first summation is for the p-adic topology. The proof of this formula relates the values of 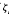p(–s, ω1+σ) for s ∈ Zp, with a branch of the ‘sth-fractional derivative’, of a suitable generating function.

MSC classification

Secondary: 11R23: Iwasawa theory 11G55: Polylogarithms and relations with $K$-theory 11R60: Cyclotomic function fields (class groups, Bernoulli objects, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 81 , Issue 2 , October 2006 , pp. 215 - 224
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Coates, J. and Wiles, A., ‘On p-adic L-functions and elliptic units’, J. Aust. Math. Soc. 26 (1978), 1–25.CrossRefGoogle Scholar
[2]Coleman, R., ‘Dilogarithms, regulators and p-adic L-functions’, Invent. Math. 69 (1982), 171–208.CrossRefGoogle Scholar
[3]Vladimirov, V., Volovich, I. and Zelemov, E., p-Adic analysis and mathematical physics (World Scientific, Singapore, 1994).CrossRefGoogle Scholar
[4]Washington, L., Introduction to cyclotomic fields, Graduate Texts in Mathematics 83, 2nd edition (Springer, New York, 1997).CrossRefGoogle Scholar