Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T09:10:35.611Z Has data issue: false hasContentIssue false
  • English
  • Français

The difference of consecutive eigenvalues

Part of: Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  09 April 2009

Hsu-Tung Ku  and
Mei-Chin Ku
Hsu-Tung Ku
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst, Massachusetts 01003, USA
Mei-Chin Ku
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst, Massachusetts 01003, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a smooth bounded domain in Rn with smooth boundary, n ≥ 2, and 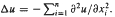. We prove an inequality involving the first k + 1 eigenvalues of the eigenvalue problem: 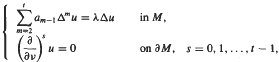where am−1 ≥ 0 are constants and at−1 = 1. We also obtain a uniform estimate of the upper bound of the ratios of consecutive eigenvalues.

MSC classification

Secondary: 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 57 , Issue 3 , December 1994 , pp. 305 - 315
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Chen, Z. C. and Qian, C. L., ‘Estimates for discrete spectrum of Laplace operators with any order’, J. China Univ. Sci. Tech. 20 (1990), 259–266.Google Scholar
[2]Hile, G. N. and Protter, M. H., ‘Inequalities for eigenvalues of the Laplacian’, Indiana Univ. Math. J. 29 (1980), 523–538.CrossRefGoogle Scholar
[3]Hile, G. N. and Yeh, R. Z., ‘Inequalities for eigenvalues of the biharmonic operators’, Pacific J. Math. 112 (1984), 115–133.CrossRefGoogle Scholar
[4]Ku, H. T. and Ku, M. C., Eigenvalue problems for higher order Laplace operators on Riemannian manifolds, mimeographed (University of Massachusetts, Amherst, 1990).Google Scholar
[5]Ku, H. T., Ku, M. C. and Tang, D. Y., ‘Inequalities for eigenvalues of elliptic equations and the generalized Polya conjecture’, J. Differential Equations 97 (1992), 127–139.CrossRefGoogle Scholar
[6]Payne, L. E., Polya, G. and Weinberger, H. F., ‘On the ratio of consecutive eigenvalues’, J. Math. Phys. 35 (1956), 289–298.CrossRefGoogle Scholar