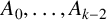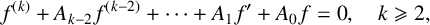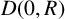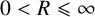DESCRIPTION OF GROWTH AND OSCILLATION OF SOLUTIONS OF COMPLEX LDE’S

Abstract

It is known that, in the unit disc as well as in the whole complex plane, the growth of the analytic coefficients $A_0,\dotsc ,A_{k-2}$ of

$$ \begin{align*} f^{(k)} + A_{k-2} f^{(k-2)} + \dotsb + A_1 f'+ A_0 f = 0, \quad k\geqslant 2, \end{align*} $$

determines, under certain growth restrictions, not only the growth but also the oscillation of the equation’s nontrivial solutions, and vice versa. A uniform treatment of this principle is given in the disc $D(0,R)$, $0<R\leqslant \infty $, by using several measures for growth that are more flexible than those in the existing literature, and therefore permit more detailed analysis. In particular, the results obtained are not restricted to cases where the solutions are of finite (iterated) order of growth in the classical sense. The new findings are based on an accurate integrated estimate for logarithmic derivatives of meromorphic functions, which preserves generality in terms of three free parameters.

1 Introduction

It is a well-known fact that the growth of analytic coefficients $A_0, \dotsc , A_{k-1}$ of the differential equation

(1-1) $$ \begin{align} f^{(k)} + A_{k-1} f^{(k-1)} + \dotsb + A_1 f'+ A_0 f = 0, \quad k\geqslant 2, \end{align} $$

restricts the growth of solutions of (1-1), and vice versa. Here we assume analyticity in the disc $D(0,R)$ , where $0<R\leqslant \infty $ . We write $\mathbb {D} = D(0,1)$ and $\mathbb {C} = D(0,\infty )$ for short. In the case $A_{k-1} \equiv 0$ the oscillation of nontrivial solutions of (1-1) provides a third property, which is known to be equivalent to the other two in certain cases [10, 16]. Recall also that there exists a standard transformation that yields $A_{k-1}\equiv 0$ and leaves the zeros of solutions invariant; see [10] and [13, page 74].

In the present paper we confine ourselves to the case $A_{k-1}\equiv 0$ . Our intention is to elaborate on new circumstances in which the growth of the Nevanlinna functions $T(r,f)$ and $N(r,1/f)$ of any nontrivial solution f of (1-1) and the growth of the quantity

(1-2) $$ \begin{align} \max_{j=0,\dotsc, k-2} \,\int_{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z) \end{align} $$

are interchangeable in an appropriate sense. Here $dm(z)$ is the standard two-dimensional Lebesgue measure. By the growth estimates for solutions of linear differential equations [9], we deduce the asymptotic inequalities

$$ \begin{align*} N(r,1/f) \lesssim 1+T(r,f) \lesssim 1 + \sum_{j=0}^{k-2} \int_{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z), \end{align*} $$

where the comparison constants depend on the initial values of f. Therefore, the problem at hand reduces to showing that, if $N(r,1/f)$ of any nontrivial solution f of (1-1) has a certain growth rate, then the quantity in (1-2) has the same or similar growth rate. An outline of the proof is as follows. The growth of Nevanlinna characteristics of quotients of linearly independent solutions can be controlled by the second main theorem of Nevanlinna and an assumption on zeros of solutions. The classical representation theorem [12] provides us with the means to express coefficients in terms of quotients of linearly independent solutions. Since this representation entails logarithmic derivatives of meromorphic functions, this argument boils down to establishing accurate integrated logarithmic derivative estimates involving several free parameters.

One of the benefits of our approach on differential equations is the freedom provided by various growth indicators. This allows us to treat a large range of growth categories by uniform generic statements. In particular, the results obtained are not restricted to cases where the solutions are of finite (iterated) order of growth in the classical sense. The other advantage is the fact that both cases of the whole complex plane and the finite disc can be covered simultaneously.

Logarithmic derivatives of meromorphic functions are considered from a new perspective which preserves generality in terms of three free parameters. Indeed, assuming that f is meromorphic in a domain containing the closure $\overline {D(0,R)}$ , we estimate area integrals of generalized logarithmic derivatives of the type

$$ \begin{align*} \int_{r'<|z|<r} \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})} \, dm(z), \end{align*} $$

where $r'<r<R$ are free, and no exceptional set occurs. Such estimates are of course also of independent interest. Our findings are accurate, as demonstrated by concrete examples, and improve results in the existing literature.

The remainder of this paper is organized as follows. The results on differential equations and on logarithmic derivatives are discussed in Sections 2 and 3, respectively. Results on logarithmic derivatives are proved in Sections 4 and 5, while the proofs of the results on differential equations are presented in Sections 6–8.

2 Results on differential equations

Let $0<R\leqslant \infty $ and $\omega \in L^1(0,R)$ . The extension defined by $\omega (z) = \omega (|z|)$ for all $z\in D(0,R)$ is called a radial weight on $D(0,R)$ . For such an $\omega $ , write $\widehat {\omega }(z) = \int _{|z|}^R \omega (s)\, ds$ for $z\in D(0,R)$ . We assume throughout the paper that $\widehat {\omega }$ is strictly positive on $[0,R)$ , for otherwise $\omega (r)=0$ for almost all r close to R, and that case is not of interest in our setting.

Our first result characterizes differential equations

(2-1) $$ \begin{align} f^{(k)} + A_{k-2} f^{(k-2)} + \dotsb + A_1 f'+ A_0 f = 0, \quad k\geqslant 2, \end{align} $$

whose solutions belong to a Bergman–Nevanlinna type space [14, 16]. The novelty of this result not only stems from the general growth indicator induced by the auxiliary functions $\Psi ,\omega ,s$ but also lies in the fact that it includes the cases of the finite disc and the whole complex plane in a single result.

Theorem 2.1. Let $\Psi :[0,\infty ) \to [0,\infty )$ be a nondecreasing function that satisfies $\Psi (x^2) \lesssim \Psi (x)$ for all $0\leqslant x< \infty $ , and $\Psi (\log x) = o(\Psi (x))$ as $x\to \infty $ . For fixed ${0<R\leqslant\infty }$ , let $s:[0,R) \to [0,R)$ be an increasing function such that $s(r)\in (r,R)$ for all ${0\leqslant r <R}$ , let $\omega $ be a radial weight such that $\widehat {\omega }(r) \lesssim \widehat {\omega }(s(r))$ for all $0\leqslant r <R$ , and assume

(2-2) $$ \begin{align} \int_0^R \Psi\bigg( s(r) \log \frac{e \, s(r)}{s(r)-r} \bigg) \, \omega(r) \, dr<\infty. \end{align} $$

If the coefficients $A_0,\dotsc ,A_{k-2}$ are analytic in $D(0,R)$ , then the following conditions are equivalent:

1. (i) $\int _0^R \Psi ( \int _{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z) ) \, \omega (r)\, dr < \infty $ for all $j=0,\dotsc ,k-2$ ;

2. (ii) $\int _0^R \Psi ( T(r,f) ) \, \omega (r) \, dr < \infty $ for all solutions f of (2-1);

3. (iii) $\int _0^R \Psi ( N(r,1/f) ) \, \omega (r) \, dr < \infty $ for all nontrivial solutions f of (2-1).

Note the following observations regarding Theorem 2.1.

1. (a) The analogues of (i) and (ii) are equivalent also for differential equation (1-1). See [5] for another general scale to measure the growth in the case of the complex plane.

2. (b) The result is relevant only when $\Psi $ is unbounded.

3. (c) The classical choices for s in the cases of $D(0,R)$ and $\mathbb {C}$ are $s(r)=(r+R)/2$ and $s(r)=2r$ , respectively. While the function s is absent in assertions (i)–(iii), its effect is implicit through the dependence in the hypothesis on s, $\Psi $ and $\omega $ . In terms of applications, the auxiliary function s provides significant freedom of possible choices of $\Psi $ and $\omega $ .

4. (d) The condition $\Psi (x^2) \lesssim \Psi (x)$ requires slow growth and local smoothness. For example, it is satisfied by any positive power of any (iterated) logarithm. To see that restrictions on the growth alone do not imply this condition, let g be any nondecreasing unbounded function. Choose a sequence $\{x_j\}_{j=1}^{\infty }$ such that $g(x_j) \geqslant 2^{2^j}$ and $x_{j+1} \geqslant x_j^2$ , and define h such that $h(x)=2^{2^j}$ for $x_j\leqslant x < x_{j+1}$ . Then g dominates h, while $h(x_n)/h(\sqrt {x_n})=2^{2^{n-1}}\to \infty $ as $n\to \infty $ .

5. (e) The assumption $\Psi (\log x) = o(\Psi (x))$ , as $x\to \infty $ , is trivial for typical choices of $\Psi $ such as $\Psi (x)=\log ^+ x$ . However, the condition is not satisfied by all continuous, increasing and unbounded functions $\Psi $ . A counterexample is given by $\Psi (x)=\log _n(x)+(n-1)(e-1)$ , $e_n(1)\leqslant x\leqslant e_{n+1}(1)$ , for which $\Psi (\log x) \sim \Psi (x)$ as $x\to \infty $ . Here $\log _n$ and $e_n$ stand for iterated logarithms and exponentials, respectively.

6. (f) For a fixed s, the requirement $\widehat {\omega }(r) \lesssim \widehat {\omega }(s(r))$ not only controls the rate at which $\widehat \omega $ decays to zero but also demands a certain local smoothness. The situation is in some sense similar to that of $\Psi $ .

7. (g) Theorem 2.1 is relevant only when some solution f of (2-1) satisfies

   $$ \begin{align*} \limsup_{r\to R^-} \, \frac{T(r,f)}{s(r)\log((e s(r))/(s(r)-r))} = \infty, \end{align*} $$
   but its applicability is not restricted to any prespecified growth scale. Indeed, if f is an arbitrary entire function, then we find a sufficiently smooth and fast-growing increasing function $\varphi $ such that its growth exceeds that of $T(r,f)$ and its inverse $\varphi ^{-1}=\Psi $ satisfies $\Psi (x^2) \lesssim \Psi (x)$ . Further, if $s(r)=2r$ and $\omega (r)=(1+r)^{-3}$ , then all requirements on $\Psi $ , $\omega $ and s are fulfilled, and
   $$ \begin{align*} \int_0^\infty \Psi( T(r,f) ) \, \omega(r) \, dr \leqslant \int_0^\infty \Psi(\varphi(r))\, \omega(r) \, dr = \int_0^\infty r\, \omega(r) \, dr< \infty. \end{align*} $$
   The case of the finite disc is similar. This shows, in particular, that Theorem 2.1 is not restricted to functions of finite iterated order in the classical sense.

Observations similar to (a)–(g) also apply for our forthcoming results.

The arguments in the proof of Theorem 2.1 also apply in the case where the growth indicators given in terms of integrals are replaced with ones stated in terms of limit superiors.

Theorem 2.2. Let $\Psi :[0,\infty ) \to [0,\infty )$ be a nondecreasing function that satisfies $\Psi (x^2) \lesssim \Psi (x)$ for all $0\leqslant x< \infty $ , and $\Psi (\log x) = o(\Psi (x))$ as $x\to \infty $ . For fixed $0<R\leqslant \infty $ , let $s:[0,R) \to [0,R)$ be an increasing function such that $s(r)\in (r,R)$ for all ${0\leqslant r <R}$ , let $\omega $ be a radial weight such that $\widehat {\omega }(r) \lesssim \widehat {\omega }(s(r))$ for all $0\leqslant r <R$ , and assume

$$ \begin{align*} \limsup_{r\to R^-} \, \Psi\bigg( s(r) \log \frac{e \, s(r)}{s(r)-r} \bigg) \, \widehat\omega(r)<\infty. \end{align*} $$

If the coefficients $A_0,\dotsc ,A_{k-2}$ are analytic in $D(0,R)$ , then the following conditions are equivalent:

1. (i) $\limsup _{r\to R^-} \, \Psi ( \int _{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z) ) \, \widehat \omega (r)\, < \infty $ for all $j=0,\dotsc ,k-2$ ;

2. (ii) $\limsup _{r\to R^-} \, \Psi ( T(r,f) ) \, \widehat \omega (r) < \infty $ for all solutions f of (2-1);

3. (iii) $\limsup _{r\to R^-} \, \Psi ( N(r,1/f) ) \, \widehat \omega (r) < \infty $ for all nontrivial solutions f of (2-1).

The proofs of Theorems 2.1 and 2.2 are similar and the latter is omitted. The small-o version of Theorem 2.2 is also valid in the sense that the finiteness of limit superiors can be replaced by the requirement that they are zero (all four of them).

Let $\widehat {\mathcal {D}}$ be the class of radial weights for which there exists a constant ${C=C(\omega )\geqslant 1}$ such that $\widehat {\omega }(r) \leqslant C \, \widehat {\omega }((1+r)/2)$ for all $0\leqslant r <1$ . Moreover, let be the class of radial weights for which there exist constants $K=K(\omega )\geqslant 1$ and $L=L(\omega )\geqslant 1$ such that $\widehat {\omega }(r) \geqslant L \, \widehat {\omega }(1-(1-r)/K)$ for all $0\leqslant r <1$ . We write for brevity. For a radial weight $\omega $ , define

$$ \begin{align*} \omega^\star(z) = \int_{|z|}^1 \omega(s) \, \log\frac{s}{|z|} \, s\, ds, \quad z\in\mathbb{D}\setminus\{0\}. \end{align*} $$

We proceed to consider an improvement of the main result in [16, Ch. 7], which concerns (2-1) in the unit disc. The following result is a far-reaching generalization of [16, Theorem 7.9] requiring much less regularity on the weight $\omega $ .

Theorem 2.3. Let $\omega \in \mathcal {D}$ . If the coefficients $A_0,\dotsc ,A_{k-2}$ are analytic in $\mathbb {D}$ , then the following conditions are equivalent:

1. (i) $\int _{\mathbb {D}} |A_j(z)|^{{1}/({k-j})} \, \widehat {\omega }(z) \, dm(z) < \infty $ for all $j=0,\dotsc ,k-2$ ;

2. (ii) ${\int _0^1} T(r,f) \, \omega (r)\, dr < \infty $ for all solutions of (2-1);

3. (iii) ${\int _0^1} N(r,1/f) \, \omega (r)\, dr < \infty $ for all nontrivial solutions of (2-1);

4. (iv) the zero sequences $\{z_k\}$ of nontrivial solutions of (2-1) satisfy $\sum _k \omega ^\star (z_k)<\infty $ .

In Theorem 2.3 we may assume that the possible value $z_k=0$ is removed from the zero sequence. Note that this result is not a consequence of Theorem 2.1, and vice versa. Roughly speaking, Theorem 2.3 corresponds to the case $\Psi (x)=x$ , which is excluded in Theorem 2.1. Also Theorem 2.1 extends to cases which cannot be reached by [16, Theorem 7.9]. We refer to the discussion at the end of [16, Ch. 7] for more details.

The counterpart of Theorem 2.3 for the complex plane is the case with polynomial coefficients, which is known in the existing literature [10]. This is also the reason why Theorem 2.3 is restricted to $\mathbb {D}$ .

Our final result on differential equations is a normed analogue of Theorem 2.2, and therefore its proof requires more detailed analysis. It is based on another limsup order, which is defined and discussed next. Let $\Psi : [0,\infty )\to \mathbb {R}^+$ and $\varphi : (0,R) \to \mathbb {R}^+$ be continuous, increasing and unbounded functions, where $0<R\leqslant \infty $ . We define the $(\Psi ,\varphi )$ -order of a nondecreasing function $\psi : (0,R) \to \mathbb {R}^+$ by

$$ \begin{align*} \rho_{\Psi,\varphi}(\psi)=\limsup_{r\to R^-}\frac{\Psi(\log^+\psi(r))}{\log\varphi(r)}. \end{align*} $$

This generalizes the $\varphi $ -order introduced in [4, 11]. If f is meromorphic in $D(0,R)$ , then the $(\Psi ,\varphi )$ -order of f is defined as $\rho _{\Psi ,\varphi }(f)=\rho _{\Psi ,\varphi }(T(r,f))$ . If $a\in \widehat {\mathbb {C}}$ , then the $(\Psi ,\varphi )$ -exponent of convergence of the a-points of f is defined as $\lambda _{\Psi ,\varphi }(a,f)=\rho _{\Psi ,\varphi }(N(r,a,f))$ . These two concepts regarding f reduce to the classical cases in the plane if $\Psi $ and $\varphi $ are identity mappings.

In contrast to Theorems 2.1 and 2.2, we suppose that $\Psi $ satisfies a subadditivity type property

(2-3) $$ \begin{align} \Psi(x+y)\leqslant \Psi(x)+\Psi(y)+O(1), \end{align} $$

which is particularly true if $\Psi (x)=x$ or $\Psi (x)=\log ^+ x$ , corresponding to the usual order and the hyper order, respectively. In fact, if $\Psi $ is a positive function such that $\Psi (x)/x$ is eventually nonincreasing, then $\Psi $ satisfies this subadditivity type property. This can be proved by writing $\Psi (x)=x \cdot (\Psi (x)/x)$ , where x is subadditive. The auxiliary function $\varphi $ gives us freedom to apply the definition of $(\Psi ,\varphi )$ -order to different growth scales. Since $T(r,fg)\leqslant 2\max \{T(r,f),T(r,g)\}$ and $T(r,f+g)\leqslant 2\max \{T(r,f),T(r,g)\}+\log 2$ for any meromorphic f and g, we conclude

(2-4) $$ \begin{align} \begin{aligned} \rho_{\Psi,\varphi}(fg) &\leqslant \max\{\rho_{\Psi,\varphi}(f),\rho_{\Psi,\varphi}(g)\},\\ \rho_{\Psi,\varphi}(f+g) &\leqslant \max\{\rho_{\Psi,\varphi}(f),\rho_{\Psi,\varphi}(g)\}. \end{aligned} \end{align} $$

Let $s:[0,R)\to [0,R)$ be an increasing function such that $s(r)\in (r,R)$ for $0\leqslant r<R$ . Using the Gol’dberg–Grinshtein estimate [2, Corollary 3.2.3], we obtain

(2-5) $$ \begin{align} T(r,f')\lesssim 1+\log^+\frac{s(r)}{r(s(r)-r)} +T(s(r),f). \end{align} $$

Suppose that $\varphi $ and s are chosen such that

$$ \begin{align*} \limsup_{r\to R^-} \, \frac{\log\varphi(s(r))}{\log\varphi(r)} = 1 \end{align*} $$

and

(2-6) $$ \begin{align} \rho_{\Psi,\varphi}\bigg(\log^+\frac{s(r)}{r(s(r)-r)}\bigg) = 0. \end{align} $$

Then

(2-7) $$ \begin{align} \rho_{\Psi,\varphi}(f') \leqslant \rho_{\Psi,\varphi}(f). \end{align} $$

Condition (2-6) is trivial for standard choices of $\Psi $ , $\varphi $ and s in the plane and in the disc $D(0,R)$ .

The validity of the reverse inequality $\rho _{\Psi ,\varphi }(f) \leqslant \rho _{\Psi ,\varphi }(f')$ is based on similar discussions as above and on the estimate

$$ \begin{align*} T(r,f)\lesssim \frac{s(r)}{s(r)-r}\bigg(\log \frac{2s(r)}{s(r)-r}\bigg)(T(s(r),f')+1)+\log^+ r \end{align*} $$

by Chuang [3]. Regarding our applications, this reverse estimate is not needed.

Theorem 2.4 below generalizes the main results in [4, 10] to some extent.

Theorem 2.4. Suppose that $\Psi $ , $\varphi $ and s are functions as above such that (2-4) and (2-7) hold, but (2-6) is replaced with the stronger condition

(2-8) $$ \begin{align} \rho_{\Psi,\varphi}\bigg(\frac{s(r)}{r} \, \log\frac{e\, s(r)}{s(r)-r}\bigg) = 0. \end{align} $$

In addition, we suppose $\rho _{\Psi ,\varphi }(\log ^+ r)=0$ and $\Psi (\log x) = o(\Psi (x))$ as $x\to \infty $ . Let $\lambda \geqslant 0$ . If the coefficients $A_0,\dotsc ,A_{k-2}$ are analytic in $D(0,R)$ , then the following conditions are equivalent:

1. (i) $\rho _{\Psi ,\varphi }(({1}/{r}) \int _{D(0,r)}|A_j(z)|^{{1}/({k-j})}\, dm(z))\leqslant \lambda $ for all $j=0,\ldots ,k-2$ ;

2. (ii) $\rho _{\Psi ,\varphi }(f)\leqslant \lambda $ for all solutions f of (2-1);

3. (iii) $\lambda _{\Psi ,\varphi }(0,f)\leqslant \lambda $ and $\rho _{\Psi ,\varphi }(f)< \infty $ for all nontrivial solutions f of (2-1).

Moreover, if a strict inequality holds in any of the three conditions above, then strict inequalities hold in the remaining two conditions.

Note the following observations regarding Theorem 2.4.

1. (a) Assumption (2-8) restricts the possible values of $s(r)$ . It requires that $s(r)$ cannot be significantly larger than r, and at the same time $s(r)-r$ cannot be too small. For example, the choices $s(r)=c r$ and $s(r)=r(\log r)^\alpha $ are allowed in the classical setting of the complex plane for any $c>1$ and $\alpha>0$ .

2. (b) The assumption $\rho _{\Psi ,\varphi }(\log ^+ r)=0$ is trivial if $R<\infty $ , while if $R=\infty $ it is equivalent to saying that all rational functions are of $(\Psi ,\varphi )$ -order zero.

3. (c) By a careful inspection of the proof of Theorem 2.4, we see that the assumptions can be significantly relaxed if the quantities in (i), (ii) and (iii) are required to be simultaneously either finite or infinite. First, (2-3) can be relaxed to $\Psi (x+y) \lesssim \Psi (x) + \Psi (y) + 1$ , which is satisfied, for instance, by $\Psi (x)=x^\alpha $ for $\alpha>1$ . Then analogues of (2-4) and (2-7) hold, where the inequality sign $\leqslant $ is replaced by  $\lesssim $ . Second, instead of (2-8) and $\rho _{\Psi ,\varphi }(\log ^+r)=0$ , it suffices to require that the orders in question are finite. In this case the $\rho _{\Psi ,\varphi }$ -order can be chosen to be the logarithmic order in the finite disc and in the complex plane.

3 Results on logarithmic derivatives

Our results on differential equations are based on new estimates on logarithmic derivatives of meromorphic functions.

Theorem 3.1. Let $0<\varrho <\infty $ and $f\not \equiv 0$ be meromorphic in a domain containing $\overline {D(0,\varrho )}$ . Then there exists a positive constant C, which depends only on the initial values of f at the origin, such that

$$ \begin{align*} \begin{aligned} & \int_{r'<|z|<r} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z)\\ & \quad \lesssim \bigg( 4 \varrho \frac{r-r'}{\varrho-r'} \bigg( 2 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + (2\pi + 2)(r-r') + 3\varrho \log\frac{\varrho-r'}{\varrho-r} \bigg) \\ & \qquad\times ( 2 T(\varrho,f) + C ), \quad 0\leqslant r' < r<\varrho. \end{aligned} \end{align*} $$

The term

$$ \begin{align*} \frac{r-r'}{\varrho-r'} \bigg( 2 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) \end{align*} $$

appearing in Theorem 3.1 is uniformly bounded above by $2+ \log {2}$ for all $0\leqslant r'< r\,{<}\,\varrho $ , and it decays to zero as $r'\to r$ . Therefore, Theorem 3.1 yields

(3-1) $$ \begin{align} \begin{aligned} \int_{r'<|z|<r} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z) & \lesssim \varrho \log\frac{e(\varrho-r')}{\varrho-r} \, ( T(\varrho,f) + 1 ), \quad 0\leqslant r'<r<\varrho. \end{aligned} \end{align} $$

The following examples illustrate the sharpness of (3-1).

Example 3.2. Let $f(z)=\exp (z^n)$ for $z\in \mathbb {C}$ , and $\varrho =2r$ . By a straightforward computation, $T(r,f)=r^n/\pi $ for $0<r<\infty $ . Now

$$ \begin{align*} \int_{|z|<r} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z) = 2\pi n \int_0^r t^n \, dt = \frac{2\pi n}{n+1} \, r^{n+1}, \quad 0<r<\infty, \end{align*} $$

while

$$ \begin{align*} \varrho \, \log\frac{e\varrho}{\varrho-r} \, ( T(\varrho,f) + 1) = 2r ( 1+ \log 2 ) \bigg( \frac{2^n r^n}{\pi} + 1\bigg), \quad 0<r<\infty. \end{align*} $$

This shows that the leading $\varrho $ in (3-1) cannot be removed.

Example 3.3. Let $f(z)=\exp (-(1+z)/(1-z))$ for $z\in \mathbb {D}$ , and $\varrho =(1+r)/2$ . By a straightforward computation, $T(r,f)=0$ for $0<r<1$ . Now

$$ \begin{align*} \int_{|z|<r} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z) = \int_{|z|<r} \frac{2}{|1-z|^2} \, dm(z) = 2\pi \log\frac{1}{1-r^2}, \quad 0<r<1, \end{align*} $$

while

$$ \begin{align*} \varrho \, \log\frac{e\varrho}{\varrho-r} \, ( T(\varrho,f) + 1) = \frac{1+r}{2} \, \log \frac{e(1+r)}{1-r}, \quad 0<r<1. \end{align*} $$

This shows that the logarithmic term in (3-1) cannot be removed.

In the special case when $\rho / r'$ is uniformly bounded an equivalent estimate (up to a constant factor) is obtained in [1, 6]. In fact, a much more general class of functions is considered in [6]. These results imply

$$ \begin{align*} \int_{r'<|z|<r} \bigg|\frac{f'(z)}{f(z)} \bigg| \, dm(z) \lesssim \rho \, \frac{r-r'}{\rho-r} \, T(\kern1.2pt \rho, f), \quad 0\leqslant r'<r<\varrho. \end{align*} $$

On the other hand, Gol’dberg and Strochik [7, Theorem 7] established a general upper estimate for the integral of the logarithmic derivative over a region of the form

$$ \begin{align*}\{te^{i\varphi }: r'<t<r, \, \varphi \in E(t)\}, \end{align*} $$

where $E=E(t)$ is a measurable subset of $[0, 2\pi ]$ with $m(E)\leqslant \theta \in (0, 2\pi ]$ . This estimate allows arbitrary values $r'<r<\rho $ , and takes into account the measure of E. Nevertheless, if $\rho /r'$ tends to infinity, $r\asymp r'$ and $\operatorname {\mathrm {mes}} E=2\pi $ , then Theorem 3.1 improves all known results, giving

$$ \begin{align*} \int_{r'<|z|<r} \bigg|\frac{f'(z)}{f(z)} \bigg| \, dm(z) \lesssim (r -r') \, T(\kern1.2pt \rho, f). \end{align*} $$

We proceed to consider two consequences of Theorem 3.1, the first of which concerns generalized logarithmic derivatives.

Corollary 3.4. Let $0<R<\infty $ and f be meromorphic in a domain containing $\overline {D(0,R)}$ . Suppose that $j,k$ are integers with $k>j\geqslant 0$ , and $f^{(\kern1.2pt j)}\not \equiv 0$ . Then

$$ \begin{align*} \int_{r'<|z|<r} \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})} \, dm(z) \lesssim R \, \log\frac{e\, (R-r')}{R-r} \, \bigg( 1 + \log^+ \frac{1}{R-r} + T(R,f)\bigg) \end{align*} $$

for $0\leqslant r' < r<R$ .

A standard argument based on Borel’s lemma transforms R back to r. In the case of  $\mathbb {D}$ , the choice $R = r + (1-r)/T(r,f)$ implies

$$ \begin{align*} T(R,f) \leqslant 2 T(r,f)\quad \text{and} \quad \log\frac{eR}{R-r} = \log \bigg( e + \frac{er \, T(r,f)}{1-r} \bigg), \end{align*} $$

the inequality being valid outside a possible exceptional set $E\subset [0,1)$ such that $\int _E dr/(1-r) < \infty $ . In the case of  $\mathbb {C}$ , the choice $R=r+1/(eT(r,f))$ implies

$$ \begin{align*} T(R,f) \leqslant 2 T(r,f) \quad \text{and} \quad \log\frac{eR}{R-r} = \log ( e + er \, T(r,f) ), \end{align*} $$

the inequality being valid outside a possible exceptional set $E\subset [0,\infty )$ such that $\int _E dr < \infty $ .

The following consequence of Theorem 3.1 generalizes [4, Theorem 5] to an arbitrary auxiliary function $s(r)\in (r,R)$ . A similar result for subharmonic functions in the plane is obtained in [6]; see also [8, Lemma 5].

Corollary 3.5. Let f be meromorphic in $D(0,R)$ for $R<\infty $ , and let $j,k$ be integers with $k>j\geqslant 0$ such that $f^{(\kern1.2pt j)}\not \equiv 0$ . Let $s:[0,R) \to [0,R)$ be an increasing continuous function such that $s(r) \in (r,R)$ and $s(r)-r$ is decreasing. If $\delta \in (0,1)$ , then there exists a measurable set $E\subset [0,R)$ with

$$ \begin{align*} \overline{d}(E) = \limsup_{r\to R^-} \, \frac{m(E \cap [r,R))}{R-r} \leqslant \delta \end{align*} $$

such that

(3-2) $$ \begin{align} \int_0^{2\pi} \bigg| \frac{f^{(k)}(re^{i\theta})}{f^{(\kern1.2pt j)}(re^{i\theta})} \bigg|^{{1}/({k-j})} \, d\theta \lesssim \frac{T(s(r),f) -\log(s(r)-r)}{s(r)-r}, \quad r\in [0,R) \setminus E. \end{align} $$

Moreover, if $k=1$ and $j=0$ , then the logarithmic term in (3-2) can be omitted.

The proof of Corollary 3.5 can easily be modified to obtain the following result.

Corollary 3.6. Let f be meromorphic in $\mathbb {C}$ , and let $j,k$ be integers with ${k>j\geqslant 0}$ such that $f^{(\kern1.2pt j)}\not \equiv 0$ . Let $S:[0,\infty ) \to [0,\infty )$ be an increasing continuous function such that $S(r) \in (r,\infty )$ and $S(r)-r$ is decreasing. If $\delta \in (0,1)$ , then there exists a measurable set $E\subset [0,\infty )$ with

$$ \begin{align*} \overline{D}(E)=\limsup_{r\to\infty}\frac{m(E \cap [0,r))}{r}\leqslant \delta \end{align*} $$

such that

(3-3) $$ \begin{align} \int_0^{2\pi} \bigg| \frac{f^{(k)}(re^{i\theta})}{f^{(\kern1.2pt j)}(re^{i\theta})} \bigg|^{{1}/({k-j})} \, d\theta \lesssim \frac{T(S(r),f) +\log S(r)-\log(S(r)-r)}{S(r)-r} \end{align} $$

for $r\in [0,\infty ) \setminus E$ . Moreover, if $k=1$ and $j=0$ , then the logarithmic terms in (3-3) can be omitted.

4 Proof of Theorem 3.1

As is the case with usual estimates for logarithmic derivatives, the proof begins with the standard differentiated form of the Poisson–Jensen formula. Differing from the proof of [4, Theorem 5], where the integration is conducted in a sequence of annuli of fixed hyperbolic width, we consider a single annulus of arbitrary width in several steps. This is due to an arbitrary $s(r)$ , as opposed to a specific $s(r)=1-\beta (1-r)$ , $\beta \in (0,1)$ , in [4, Theorem 5].

By the Poisson–Jensen formula,

$$ \begin{align*} \begin{aligned} \log{|f(z)|} & = \frac{1}{2\pi} \int_0^{2\pi} \log |f(\varrho e^{i\varphi})| \, K(z,\varrho e^{i\varphi}) \, d\varphi\\ & \quad - \sum_{|a_\mu | < \varrho} \log \, \bigg| \frac{\varrho^2-\overline{a}_\mu z}{\varrho(z-a_\mu)} \bigg| + \sum_{|b_\nu | < \varrho} \log \, \bigg| \frac{\varrho^2-\overline{b}_\nu z}{\varrho(z-b_\nu)} \bigg|, \quad z\in D(0,\varrho), \end{aligned} \end{align*} $$

where $\{a_\mu \}$ and $\{b_\nu \}$ are the zeros and the poles of f, and

$$ \begin{align*} K(z,\varrho e^{i\varphi}) = \frac{\varrho^2 - |z|^2}{|\varrho e^{i\varphi} - z|^2} = \operatorname{\mathrm{Re}} \!\bigg( \frac{\varrho e^{i\varphi} +z }{\varrho e^{i\varphi} - z} \bigg), \quad z\in D(0,\varrho), \end{align*} $$

is the Poisson kernel. By differentiation,

$$ \begin{align*} \begin{aligned} \frac{f'(z)}{f(z)} & = \frac{1}{2\pi} \int_0^{2\pi} \log |f(\varrho e^{i\varphi})| \, \frac{2\varrho e^{i\varphi}}{(\varrho e^{i\varphi}-z)^2} \, d\varphi\\ & \quad - \sum_{|a_\mu | < \varrho} \frac{|a_\mu|^2-\varrho^2}{(z-a_\mu)(\varrho^2-\overline{a}_\mu z)} + \sum_{|b_\nu | < \varrho} \frac{|b_\nu|^2-\varrho^2}{(z-b_\nu)(\varrho^2-\overline{b}_\nu z)} \end{aligned} \end{align*} $$

for all $z\in D(0,\varrho )$ . Let $\{ c_m \} = \{a_\mu \} \cup \{ b_\nu \}$ . We deduce

$$ \begin{align*} \bigg| \frac{f'(z)}{f(z)} \bigg| \leqslant \frac{\varrho}{\pi} \int_0^{2\pi} \frac{| \log |f(\varrho e^{i\varphi})||}{|\varrho e^{i\varphi}-z|^2} \, d\varphi + \sum_{|c_m | < \varrho} \frac{\varrho^2 - |c_m|^2}{|z-c_m|\, |\varrho^2-\overline{c}_m z|}, \quad z\in D(0,\varrho), \end{align*} $$

and therefore an application of Fubini’s theorem yields

(4-1) $$ \begin{align} & \hspace{-90pt}\int_{r'<|z|<r} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z)\qquad\qquad \end{align} $$

(4-2) $$ \begin{align} & \quad \leqslant \frac{\varrho}{\pi} \int_0^{2\pi} |\!\log |f(\varrho e^{i\varphi})|| \bigg( \, \int_{r'<|z|<r} \frac{dm(z)}{|\varrho e^{i\varphi}-z|^2} \bigg)\, d\varphi \\[2pt] & \qquad + n(0) \int_{r'<|z|<r}\frac{dm(z)}{|z|}\notag\\[2pt] & \qquad + \sum_{0<|c_m | < \varrho} \frac{\varrho^2-|c_m|^2}{|c_m|} \, \int_{r'<|z|<r} \frac{dm(z)}{|z-c_m|\, |z-\varrho^2/\overline{c}_m|}, \notag \end{align} $$

where $n(r)$ is the nonintegrated counting function for $c_m$ -points in $|z|\leqslant r$ , while $N(r)$ is its integrated counterpart. Let $I_1$ be the first term on the right-hand side of (4-2), and let $I_2$ be the remaining part of the upper bound.

We proceed to study $I_1=I_1(r',r,\varrho )$ and $I_2=I_2(r',r,\varrho )$ separately. By the well-known properties of the Poisson kernel,

$$ \begin{align*} \int_{r'<|z|<r} \frac{dm(z)}{|\varrho e^{i\varphi}-z|^2} = 2\pi \int_{r'}^r \frac{s\, ds}{\varrho^2-s^2} = \pi \, \log \frac{\varrho^2-(r')^2}{\varrho^2-r^2}, \end{align*} $$

and therefore

$$ \begin{align*} I_1 & \leqslant \varrho \, \log \frac{\varrho^2-(r')^2}{\varrho^2-r^2} ( 2\, T(\varrho, f) + O(1) ). \end{align*} $$

Here $O(1)$ is a bounded term, which depends on the initial values of f at the origin and which arises from the application of Nevanlinna’s first main theorem.

To estimate $I_2$ , we need to find an upper bound for

(4-3) $$ \begin{align} \int_{r'<|z|<r} \frac{dm(z)}{|z-c|\, |z-\varrho^2/c|}, \quad 0<c<\varrho. \end{align} $$

The remaining argument is divided into separate cases. Before going any further, we consider two auxiliary results that we use to complete the proof of the theorem.

Lemma 4.1. Let $0\leqslant s_1\leqslant s_2<1$ and $0<p,q<\infty $ . Then

$$ \begin{align*} J(s_1,s_2) :=\int_0^{2\pi} \frac{d\theta}{|1-s_1 e^{i\theta}|^p \, |1-s_2 e^{i\theta}|^q} \end{align*} $$

has the following asymptotic behavior:

1. (i) if $q>1$ , then $J(s_1,s_2) \asymp {1}/{((1-s_1)^p(1-s_2)^{q-1})}$ ;

2. (ii) if $q=1$ , then $J(s_1,s_2) \asymp ({1}/{(1-s_1)^p})(\log ({1-s_1})/({1-s_2}) + 1 )$ ;

3. (iii) if $0<q<1$ , then $J(s_1,s_2) \asymp {1}/{(1-s_1)^{p+q-1}}$ .

Proof. The case $0\leqslant s_1 \leqslant s_2 < 1/2$ is trivial, and the case $0\leqslant s_1 < 1/2\leqslant s_2<1$ reduces to the classical result [19, page 226]. Therefore, we may assume $1/2 \leqslant s_1\!\leqslant s_2<1$ . By utilizing the first three nonzero terms of cosine’s Taylor series expansion, we obtain

$$ \begin{align*} |1-s e^{i\theta}|^2 = 1 + s^2 - 2s\cos\theta \geqslant (1-s)^2+\tfrac{11}{12} \, s \theta^2, \quad 0<\theta<1. \end{align*} $$

Since $s_1$ and $s_2$ are positive, the asymptotic behavior of $J(s_1,s_2)$ is comparable to that of

$$ \begin{align*} & \int_0^{1} \frac{d\theta}{|1-s_1 e^{i\theta}|^p \, |1-s_2 e^{i\theta}|^q} \\ & \quad \leqslant \bigg[ \int_0^{1-s_2} \!+ \int_{1-s_2}^{1-s_1} \!+ \int_{1-s_1}^1 \bigg] \frac{d\theta}{( (1-s_1)^2+\frac{11}{12} s_1 \theta^2 )^{{p}/{2}} ( (1-s_2)^2+\frac{11}{12} s_2 \theta^2 )^{{q}/{2}}}\\ & \quad \lesssim \frac{1-s_2}{(1-s_1)^p(1-s_2)^q} + \frac{1}{(1-s_1)^p} \int_{1-s_2}^{1-s_1} \frac{d\theta}{\theta^q} + \int_{1-s_1}^1 \frac{d\theta}{\theta^{p+q}}, \end{align*} $$

which has to be estimated in all cases (i)–(iii). The details are left to the reader. For the converse asymptotic inequality, take only the first two nonzero terms of cosine’s Taylor series expansion, and repeat the argument.

Lemma 4.2. Let $1\leqslant a < b \leqslant \infty $ . Then

$$ \begin{align*} \int_a^b \frac{\log t}{t(t-1)}\, dt \leqslant \lim_{t\to b^-} \frac{t-a}{at} \, (2+\log a), \quad \int_a^b \frac{\log t}{t^2}\, dt \leqslant \lim_{t\to b^-} \frac{t-a}{at} \, (1+\log a). \end{align*} $$

Proof. We prove the former integral estimate and leave the latter to the reader. Let $1<b<\infty $ . Then

$$ \begin{align*} \int_a^b \frac{\log t}{t(t-1)}\, dt & \leqslant \int_a^b \frac{1+\log t}{t^2} \, dt = \frac{b-a}{ab} \bigg( 2 + \frac{b \log a - a \log b}{b-a} \bigg)\\ & \leqslant \frac{b-a}{ab} \, (2+\log a). \end{align*} $$

The case $b=\infty $ is an immediate modification of the above.

With the help of Lemmas 4.1 and 4.2, we return to the proof of Theorem 3.1 and continue to estimate $I_2$ .

4.1 Case $0\leqslant r' < r \leqslant c < \varrho $

Denote $x=c/\varrho $ for short. By a change of variable, the integral in (4-3) can be transformed into

$$ \begin{align*} \int_{{r'}/{\varrho} < |w| < {r}/{\varrho}} \frac{dm(w)}{|w-x| \, |w-1/x|} = \int_{r'/\varrho}^{r/\varrho} \bigg( \int_0^{2\pi} \frac{d\theta}{|1-\frac{s}{x} e^{i\theta}| \, | 1-sx e^{i\theta}| }\bigg) s\, ds. \end{align*} $$

Let $t(s) = (1-sx)/(1-s/x)$ , and note that t is increasing for $s\in [0,x)$ . Therefore, ${t(s) \geqslant 1}$ for all $s\in [0,x)$ . By Lemma 4.1, we deduce

$$ \begin{align*} \int_{r'<|z|<r} \frac{dm(z)}{|z-c|\, |z-\varrho^2/c|} \lesssim \frac{rc}{\varrho^2} \int_{t(r'/\varrho)}^{t(r/\varrho)} \frac{\log t}{t(t-x^2)} \, dt + \frac{r}{c} \, \log\frac{\varrho^2-c r'}{\varrho^2-c r}. \end{align*} $$

An application of Lemma 4.2 yields

$$ \begin{align*} & \int_{r'<|z|<r} \frac{dm(z)}{|z-c|\, |z-\varrho^2/c|}\\ & \quad \lesssim \frac{rc}{\varrho^2} \cdot \frac{t(r/\varrho)-t(r'/\varrho)}{t(r/\varrho) \, t(r'/\varrho)} ( 2+\log t(r'/\varrho) ) + \frac{r}{c} \, \log\frac{\varrho^2-c r'}{\varrho^2-c r} \\ & \quad \leqslant \frac{c}{\varrho} \cdot \frac{r-r'}{\varrho-r'} \bigg( 2+\log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + \frac{r}{c} \, \log\frac{\varrho^2-c r'}{\varrho^2-c r}. \end{align*} $$

4.2 Case $0\leqslant r' \leqslant c< r < \varrho $

We write

$$ \begin{align*} \int_{r'< |z| < r} \frac{dm(z)}{|z-c| \, | z - \varrho^2/c|} & = \int_{r'/\varrho}^x \bigg( \int_0^{2\pi} \frac{d\theta}{|1-\frac{s}{x} e^{i\theta}| \, |1-sxe^{i\theta}|} \bigg) s\, ds\\ & \quad + x \int_x^{r/\varrho} \bigg( \int_0^{2\pi} \frac{d\theta}{|1-\frac{x}{s} e^{i\theta}| \, |1-sxe^{i\theta}|} \bigg)\, ds. \end{align*} $$

The first integral is estimated similarly to the case above:

$$ \begin{align*} & \int_{r'/\varrho}^x \bigg( \int_0^{2\pi} \frac{d\theta}{|1-\frac{s}{x} e^{i\theta}| \, |1-sxe^{i\theta}|} \bigg) s\, ds\\ & \quad \lesssim \frac{c^2}{\varrho^2} \int_{t(r'/\varrho)}^{\infty} \frac{\log t}{t(t-x^2)} \, dt + \log\frac{\varrho^2-c r'}{\varrho^2-c^2}\\ & \quad \leqslant \frac{c}{\varrho} \cdot \frac{r-r'}{\varrho-r'} \bigg( 2+\log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + \log\frac{\varrho^2-c r'}{\varrho^2-c^2}. \end{align*} $$

To the second integral we apply Lemma 4.1 and obtain

$$ \begin{align*} x \int_x^{r/\varrho} \bigg( \int_0^{2\pi} \!\frac{d\theta}{|1-\frac{x}{s} e^{i\theta}| \, |1-sxe^{i\theta}|} \bigg)\, ds \asymp x \int_x^{r/\varrho} \!\!\frac{1}{1-sx} \bigg( \log\frac{1-sx}{1-x/s} + 1\bigg)\, ds, \end{align*} $$

which will be integrated in two parts. By Lemma 4.2, the first part gives

$$ \begin{align*} x \int_x^{r/\varrho} \frac{1}{1-sx} \, \log\frac{1-sx}{1-x/s} ds & \leqslant \frac{c}{\varrho} \int_{({\varrho^2-cr})/{\varrho(r-c)}}^\infty \frac{\log t}{t (t+x)} \, dt \leqslant \frac{c}{\varrho} \int_{({\varrho^2-cr})/{\varrho(r-c)}}^\infty \frac{\log t}{t^2} \, dt\\ & \leqslant \frac{c}{\varrho} \cdot \frac{\varrho(r-c)}{\varrho^2-cr} \bigg( 1 + \log \frac{\varrho^2-cr}{\varrho(r-c)} \bigg)\\ & \leqslant \frac{c}{\varrho} \cdot \frac{r-r'}{\varrho-r'} \bigg( 1+\log 2 + \log \frac{\varrho-r'}{r-r'} \bigg), \end{align*} $$

while the second part is

$$ \begin{align*} x \int_x^{r/\varrho} \frac{1}{1-sx} \, ds = \log\frac{\varrho^2 - c^2}{\varrho^2-cr}. \end{align*} $$

In conclusion,

$$ \begin{align*} \int_{r'< |z| < r} \frac{dm(z)}{|z-c| \, | z - \varrho^2/c|} & \lesssim 2 \, \frac{c}{\varrho} \, \frac{r-r'}{\varrho-r'} \bigg( 2+\log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + \log\frac{\varrho^2 - c r'}{\varrho^2-cr}. \end{align*} $$

4.3 Case $0<c < r' < r < \varrho $

As above, by Lemma 4.2, we deduce

$$ \begin{align*} & \int_{r'< |z| < r} \frac{dm(z)}{|z-c| \, | z - \varrho^2/c|} \\[4pt] & \quad \lesssim x \int_{r'/\varrho}^{r/\varrho} \frac{1}{1-sx} \, \log\frac{1-sx}{s-x} \, ds + x \int_{r'/\varrho}^{r/\varrho} \frac{1}{1-sx} \, ds\\[4pt] & \quad = \frac{c}{\varrho} \int_{({\varrho^2-cr})/{\varrho(r-c)}}^{({\varrho^2-cr'})/{\varrho(r'-c)}} \frac{\log t}{t (t+x)} \, dt + \log\frac{\varrho^2-cr'}{\varrho^2-cr}\\[4pt] & \quad \leqslant \frac{c}{\varrho} \cdot \frac{\varrho(\varrho^2-c^2)(r-r')}{(\varrho^2-cr)(\varrho^2-cr')} \bigg( 1 + \log \frac{\varrho^2-cr}{\varrho(r-c)} \bigg)+ \log\frac{\varrho^2-cr'}{\varrho^2-cr}\\[4pt] & \quad \leqslant 2 \cdot \frac{c}{\varrho} \cdot \frac{r-r'}{\varrho-r'} \bigg( 1 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + \log\frac{\varrho^2-cr'}{\varrho^2-cr}. \end{align*} $$

The estimates from the three cases above can be combined into

$$ \begin{align*} \begin{aligned} & \int_{r'<|z|<r} \frac{dm(z)}{|z-c_m|\, |z-\varrho^2/\overline{c}_m|}\\[4pt] & \quad \lesssim \frac{2|c_m|}{\varrho} \cdot \frac{r-r'}{\varrho-r'} \bigg( 2 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + \log\frac{\varrho^2 - |c_m| r'}{\varrho^2-|c_m|r} \end{aligned} \end{align*} $$

for any $0<|c_m|<\varrho $ . This puts us in a position to estimate $I_2$ . We deduce

$$ \begin{align*} I_2 & \lesssim 2\pi (r-r')\, n(0) + \frac{2}{\varrho} \, \frac{r-r'}{\varrho-r'} \bigg( 2 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) \sum_{\varepsilon<|c_m | < \varrho} ( \varrho^2-|c_m|^2 )\\ & \quad + \sum_{\varepsilon<|c_m | < \varrho} \frac{\varrho^2-|c_m|^2}{|c_m|}\, \log\frac{\varrho^2 - |c_m| r'}{\varrho^2-|c_m|r}, \end{align*} $$

where $0<\varepsilon <\varrho $ is chosen such that there are no $c_m$ -points in $D(0,\varepsilon )\setminus \{0\}$ . We write the sums as Riemann–Stieltjes integrals and then integrate by parts, which yields

$$ \begin{align*} \sum_{\varepsilon<|c_m | < \varrho} ( \varrho^2-|c_m|^2 ) \leqslant 2 \varrho^2 \int_\varepsilon^\varrho \frac{n(t)}{t} \, dt \leqslant 2 \varrho^2 ( 2 T(\varrho,f) + O(1) ). \end{align*} $$

By using the estimate $\log x \leqslant x -1$ , which holds for any positive x, we obtain

$$ \begin{align*} & \sum_{\varepsilon<|c_m | < \varrho} \frac{\varrho^2-|c_m|^2}{|c_m|}\, \log\frac{\varrho^2 - |c_m| r'}{\varrho^2-|c_m|r}\\ & \quad \leqslant 2 \int_\varepsilon^\varrho \log\frac{\varrho^2 - t r'}{\varrho^2- tr} \, n(t) \, dt + \int_\varepsilon^\varrho \frac{\varrho^2-t^2}{t}\, \log\frac{\varrho^2 - tr'}{\varrho^2-tr} \, \frac{n(t)}{t}\, dt\\ & \quad \leqslant \bigg( 2 \varrho \log\frac{\varrho - r'}{\varrho- r} + 2 (r-r') \bigg) ( 2 T(\varrho,f) + O(1) ). \end{align*} $$

Putting together the estimates obtained, we deduce

$$ \begin{align*} \begin{aligned} I_2 & \lesssim \bigg( 4 \varrho \frac{r-r'}{\varrho-r'} \bigg( 2 + \log 2 + \log \frac{\varrho-r'}{r-r'} \bigg) + (2\pi + 2)(r-r') + 2\varrho \log\frac{\varrho-r'}{\varrho-r} \bigg)\\ & \quad \times ( 2 T(\varrho,f) + O(1) ), \quad 0\leqslant r'<r<\varrho. \end{aligned} \end{align*} $$

This completes the proof of Theorem 3.1.

5 Proofs of Corollaries 3.4 and 3.5

The following proof is a straightforward application of Theorem 3.1, or more precisely, the estimate (3-1).

Proof of Corollary 3.4.

Let $\varrho _0=r$ and $\varrho _{j+1} = (R+\varrho _j)/2$ for $j=0,\dotsc ,m-1$ . Using the estimate (2-5) inductively, we conclude

$$ \begin{align*} T(\varrho_1, f^{(m)}) & \lesssim 1 + \log^+ \frac{\varrho_2}{\varrho_1(\varrho_2-\varrho_1)} + T(\varrho_2,f^{(m-1)})\\ & \lesssim \dotsb \lesssim 1 + \log^+\frac{1}{R-r} + T(R,f) \end{align*} $$

for any $m=j, \dotsc , k-1$ . By Hölder’s inequality and (3-1),

$$ \begin{align*} \int_{r'<|z|<r} \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})} \, dm(z) & \leqslant \prod_{m=j}^{k-1} \bigg( \int_{r'<|z|<r} \bigg| \frac{f^{(m+1)}(z)}{f^{(m)}(z)} \bigg| \, dm(z)\bigg)^{{1}/({k-j})}\\ & \lesssim \prod_{m=j}^{k-1} \bigg( \varrho_1 \log\frac{e(\varrho_1-r')}{\varrho_1-r} \, ( T(\varrho_1,f^{(m)}) + 1 ) \bigg)^{{1}/({k-j})}. \end{align*} $$

The assertion follows by combining the estimates obtained.

Proof of Corollary 3.5.

We consider the case $k=1$ and $j=0$ only. The general case follows as in the proof of Corollary 3.4. Define the sequence $\{r_n\}_{n=0}^\infty $ such that $r_0=R/2$ and

(5-1) $$ \begin{align} r_n = \frac{r_{n-1}+s(r_{n-1})}{2} = r_{n-1} + \frac{1}{2} \, ( s(r_{n-1}) - r_{n-1}), \quad n\in\mathbb{N}. \end{align} $$

Since $\{r_n\}_{n=0}^\infty \subset [1/2,R)$ is increasing, there exists a limit $\lim _{n\to \infty } r_n = \alpha \leqslant R$ . Equation (5-1) implies $2\alpha =\alpha + s(\alpha )$ , which is possible only if $\alpha =R$ . We conclude ${\lim _{n\to \infty } r_n=R}$ .

By (3-1), we obtain

$$ \begin{align*} \int_{r_{n-1}<|z|<r_n} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z) & \lesssim \log\frac{e(s(r_{n-1})-r_{n-1})}{s(r_{n-1})-r_n} \, ( T(s(r_{n-1}),f) + 1 )\\ & \lesssim T(s(r_{n-1}),f) + 1, \quad n\in\mathbb{N}. \end{align*} $$

Let

$$ \begin{align*} G_n = \bigg\{ r \in [r_{n-1},r_n) : \int_0^{2\pi} \bigg| \frac{f'(re^{i\theta})}{f(re^{i\theta})} \bigg| d\theta \geqslant K \, \frac{T(s(r_{n-1}),f) + 1}{ r_{n-1} (r_n-r_{n-1})} \bigg\}, \quad n\in\mathbb{N}, \end{align*} $$

where K is a positive constant defined later. By the Chebyshev–Markov inequality,

$$ \begin{align*} \int_{r_{n-1}<|z|<r_n} \bigg| \frac{f'(z)}{f(z)} \bigg| \, dm(z) & \geqslant K \, \frac{T(s(r_{n-1}),f) + 1}{ r_{n-1} (r_n-r_{n-1})} \, \int_{G_n}\, r\, dr\\ & \geqslant K \, \frac{T(s(r_{n-1}),f) + 1}{ (r_n-r_{n-1})} \, m(G_n), \quad n\in\mathbb{N}. \end{align*} $$

Therefore, $m(G_n) \lesssim K^{-1} (r_n-r_{n-1})$ for $n\in \mathbb {N}$ . Define $E = [0,R/2) \cup \bigcup _{n\in \mathbb {N}} G_n$ .

If $r\in [r_{n-1},r_n)$ for $n\in \mathbb {N}$ , then

$$ \begin{align*} \frac{m( E \cap [r,R))}{R-r} \lesssim \frac{1}{K} \cdot \frac{\sum_{k=n}^\infty (r_k-r_{k-1})}{R-r_n} \leqslant \frac{1}{K} \cdot \frac{ s(r_{n-1}) -r_{n-1}}{s(r_{n-1})-r_n} = \frac{2}{K}. \end{align*} $$

Here we use the property that $x \mapsto (x-r_{n-1})/(x-r_n)$ is decreasing and positive for $x>r_n$ . We deduce $\overline {d}(E) \leqslant \delta $ , if $0<K<\infty $ is sufficiently large. If $r\in [r_{n-1},r_n) \setminus E$ for $n\in \mathbb {N}$ , then

$$ \begin{align*} \int_0^{2\pi} \bigg| \frac{f'(re^{i\theta})}{f(re^{i\theta})} \bigg| d\theta \leqslant K \, \frac{T(s(r_{n-1}),f) + 1}{ r_{n-1} (r_n-r_{n-1})} \leqslant \frac{4K}{R}\,\frac{T(s(r_{n-1}),f) + 1}{s(r_{n-1})-r_{n-1}}. \end{align*} $$

The assertion follows since $r\mapsto T(s(r),f)$ is increasing and $r \mapsto s(r)-r$ is decreasing.

6 Proof of Theorem 2.4

Before the proof of Theorem 2.4, we consider auxiliary results.

Theorem 6.1 [12, Theorem 2.1].

Let $f_1,\ldots ,f_k$ be linearly independent solutions of (2-1), where $A_0,\ldots ,A_{k-2}$ are analytic in $D(0,R)$ . Let

(6-1) $$ \begin{align} y_1=\frac{f_1}{f_k},\ \ldots ,\ y_{k-1}=\frac{f_{k-1}}{f_k}, \end{align} $$

and let $W_j$ be the determinant defined by

(6-2) $$ \begin{align} W_j=\left| \begin{array}{cccc} y_1'\ & y_2'\ & \cdots \ & y_{k-1}'\\ \vdots & \vdots && \vdots \\ y_1^{(\kern1.2pt j-1)}\ & y_2^{(\kern1.2pt j-1)}\ & \cdots & y_{k-1}^{(\kern1.2pt j-1)}\\[6pt] y_1^{(\kern1.2pt j+1)}\ & y_2^{(\kern1.2pt j+1)}\ & \cdots & y_{k-1}^{(\kern1.2pt j+1)}\\ \vdots & \vdots& \ddots &\vdots\\ y_1^{(k)}\ & y_2^{(k)}\ & \cdots & y_{k-1}^{(k)} \end{array} \right|,\quad j=1,\ldots, k. \end{align} $$

Then

(6-3) $$ \begin{align} A_j=\sum_{i=0}^{k-j} (-1)^{2k-i}\delta_{ki}\left(\begin{array}{c} k-i\\ k-i-j\end{array}\right) \frac{W_{k-i}}{W_k} \frac{(\sqrt[k]{W_k})^{(k-i-j)}}{\sqrt[k]{W_k}} \end{align} $$

for all $j=0,\ldots ,k-2$ , where $\delta _{kk}=0$ and $\delta _{ki}=1$ otherwise.

For a fixed branch of the kth root, there exists a constant $C\in \mathbb {C}\setminus \{0\}$ such that

(6-4) $$ \begin{align} \sqrt[k]{W_k}=\frac{1}{Cf_k}; \end{align} $$

see [12, Eq. (2.6)]. This shows that $\sqrt [k]{W_k}$ is a well-defined meromorphic function in $D(0,R)$ . For an alternative way to write the coefficients $A_0,\ldots ,A_{k-2}$ in terms of the solutions of (2-1), see [13, Proposition 1.4.7].

Lemma 6.2. Let $r<s(r)<R$ , and let $g_1,\ldots , g_k$ be linearly independent meromorphic solutions of the linear differential equation

(6-5) $$ \begin{align} g^{(k)}+B_{k-1}g^{(k-1)}+\cdots +B_1g'+B_0g=0 \end{align} $$

with coefficients $B_0,\ldots ,B_{k-1}$ meromorphic in $D(0,R)$ . Then

$$ \begin{align*} \int_{D(0,r)} |B_j(z)|^{{1}/({k-j})}\, dm(z) \lesssim s(r) \log \frac{e\, s(r)}{s(r)-r} ( S(r)+\max_{1\leqslant l\leqslant k} T(s(r),g_l) ), \end{align*} $$

for all $j=0,\ldots ,k-1$ . Here

$$ \begin{align*} S(r)=1+\log^+\frac{1}{s(r)-r}. \end{align*} $$

Proof. We follow the reasoning used in proving [13, Lemma 7.7], originally developed by Frank and Hennekemper. We proceed by induction, starting from the case $k=1$ . Hence, we suppose that $B_0$ is meromorphic in $D(0,R)$ , and that $g'+B_0g=0$ has a nontrivial meromorphic solution $g_1$ . Then Corollary 3.4, applied to $|B_0(z)|=|g_1'(z)/g_1(z)|$ , gives us the assertion at once. The more general case $g^{(k)}+B_0g=0$ with no middle-term coefficients follows similarly.

Suppose next that we have proved the case $k=n\geqslant 1$ . That is, we suppose that we have proved the assertion for n linearly independent meromorphic functions $g_1,\ldots ,g_n$ solving

$$ \begin{align*} g^{(n)}+B_{n,n-1}g^{(n-1)}+\cdots+B_{n,1}g'+B_{n,0}g=0 \end{align*} $$

with coefficients $B_{n,0},\ldots ,B_{n,n-1}$ that are meromorphic in $D(0,R)$ . Observe that the coefficients $B_{n,0},\ldots ,B_{n,n-1}$ are uniquely determined by

(6-6) $$ \begin{align} B_{n,j}=-W(g_1,\ldots,g_n)^{-1}W_j(g_1,\ldots, g_n),\quad j=0,\ldots,n-1; \end{align} $$

see [13, Proposition 1.4.7]. Note that $W_j$ has a different meaning in Kim’s result.

Consider $n+1$ linearly independent meromorphic functions $g_1,\ldots ,g_n,g_{n+1}$ . Clearly, the Wronskian determinants $W(g_1,\ldots ,g_n)$ and $W(g_1,\ldots ,g_{n+1})$ do not vanish identically. Denote

(6-7) $$ \begin{align} h_{n+1}=\bigg(\frac{d}{dz}\frac{W(g_1,\ldots,g_{n+1})}{W(g_1,\ldots,g_n)}\bigg) \bigg/\bigg(\frac{W(g_1,\ldots,g_{n+1})}{W(g_1,\ldots,g_n)}\bigg). \end{align} $$

Let g be an arbitrary meromorphic function. Expanding $W(g_1,\ldots ,g_{n+1},g)$ according to the last column starting from the bottom right corner (which is associated with a positive sign in the checkerboard pattern of signs for determinants), we get

(6-8) $$ \begin{align} \frac{W(g_1,\ldots,g_{n+1},g)}{W(g_1,\ldots,g_{n+1})}=g^{(n+1)}+\sum_{j=0}^nB_{n+1,j}g^{(\kern1.2pt j)}, \end{align} $$

where

(6-9) $$ \begin{align} B_{n+1,j}=-W(g_1,\ldots,g_{n+1})^{-1}W_j(g_1,\ldots, g_{n+1}),\quad j=0,\ldots,n. \end{align} $$

In particular, if $g\in \{g_1,\ldots ,g_{n+1}\}$ , then $W(g_1,\ldots ,g_{n+1},g)\equiv 0$ , and we see from (6-8) that the functions $g_1,\ldots ,g_n,g_{n+1}$ are linearly independent meromorphic solutions of the equation

$$ \begin{align*} g^{(n+1)}+\sum_{j=0}^nB_{n+1,j}g^{(\kern1.2pt j)}=0, \end{align*} $$

where the coefficients are given by (6-9).

Next we do some elementary computations with the Wronskian determinants appearing in the left-hand side of (6-8) (see [13, pages 134–135]) and obtain the following representation for the right-hand side of (6-8):

$$ \begin{align*} & g^{(n+1)}+\sum_{j=0}^nB_{n+1,j}g^{(\kern1.2pt j)} \\ & \quad = g^{(n+1)}+(B_{n,n-1}-h_{n+1})g^{(n)}\\ & \quad \quad +\sum_{j=1}^{n-1}(B_{n,j}'+B_{n,j-1}-B_{n,j}h_{n+1})g^{(\kern1.2pt j)} +(B_{n,0}'-B_{n,0}h_{n+1})g. \end{align*} $$

Comparing the corresponding coefficients, we deduce

(6-10) $$ \begin{align} \begin{cases} B_{n+1,n} = B_{n,n-1}-h_{n+1},\\ B_{n+1,j} = B_{n,j}'+B_{n,j-1}-B_{n,j}h_{n+1},\quad j=1,\ldots,n-1,\\ B_{n+1,0} = B_{n,0}'-B_{n,0}h_{n+1}. \end{cases} \end{align} $$

Hölder’s inequality yields

$$ \begin{align*} \begin{aligned} \int_{D(0,r)} &|B_{n+1,0}(z)|^{{1}/({n+1})}\, dm(z)\\ &\leqslant \bigg(\int_{D(0,r)}\bigg|\frac{B_{n,0}'(z)}{B_{n,0}(z)}\bigg|\, dm(z)\bigg)^{{1}/({n+1})} \bigg(\int_{D(0,r)}|B_{n,0}(z)|^{{1}/{n}}\, dm(z)\bigg)^{{n}/({n+1})}\\ &\quad+\bigg(\int_{D(0,r)}|B_{n,0}(z)|^{{1}/{n}}\, dm(z)\bigg)^{{n}/({n+1})} \bigg(\int_{D(0,r)}|h_{n+1}(z)|\, dm(z)\bigg)^{{1}/({n+1})}. \end{aligned} \end{align*} $$

Using (6-6) and Corollary 3.4, as well as (2-5), we get

$$ \begin{align*} \begin{aligned} \int_{D(0,r)} \bigg|\frac{B_{n,0}'(z)}{B_{n,0}(z)}\bigg|\,\, dm(z) & \lesssim s(r) \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant n} T(s(r),g_l) ). \end{aligned} \end{align*} $$

Here we have also applied the proof of Corollary 3.4 by introducing sufficiently many $\varrho _j$ . Analogously, from (6-7) and Corollary 3.4 it follows that

$$ \begin{align*} \int_{D(0,r)} |h_{n+1}(z)|\,dm(z) \lesssim s(r) \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant n} T(s(r),g_l) ). \end{align*} $$

The induction assumption applies for $B_{n,0}$ , so that, putting all estimates for $B_{n+1,0}$ together, we deduce the right magnitude of growth. The remaining coefficients $B_{n+1,j}$ , $j=1,\ldots ,n$ , in (6-10) can be estimated similarly. This completes the proof of the case $k=n+1$ .

Proof of Theorem 2.4.

Suppose that (i) holds. By the growth estimates [9, Corollary 5.3],

$$ \begin{align*} m(r,f) \lesssim \sum_{j=0}^{k-1} \int_0^r \int_0^{2\pi} |A_j(se^{i\theta})|^{{1}/({k-j})} \, d\theta\, ds + 1. \end{align*} $$

By applying the subharmonicity and by integrating over the interval $(0,r)$ in two parts,

$$ \begin{align*} & r \int_0^r \int_0^{2\pi} |A_j(se^{i\theta})|^{{1}/({k-j})} \, d\theta \,ds \\ & \quad \leqslant \frac{r^2}{2} \int_0^{2\pi} \bigg|A_j\bigg(\frac{r}{2}e^{i\theta}\bigg)\bigg|^{{1}/({k-j})} d\theta \cdot \frac{\int_{r/2}^r s\, ds}{\frac{3}{8} r^2}+ 2 \int_{r/2}^r \int_0^{2\pi} |A_j(se^{i\theta})|^{{1}/({k-j})} \, d\theta s\, ds, \end{align*} $$

and therefore

(6-11) $$ \begin{align} T(r,f) \lesssim \frac{1}{r} \sum_{j=0}^{k-1} \int_{D(0,r)} |A_j(se^{i\theta})|^{{1}/({k-j})} \, dm(z) + 1. \end{align} $$

The implication from (i) to (ii) follows from the properties of $\Psi $ . The implication from (ii) to (iii) is trivial because of $\lambda _{\Psi ,\varphi }(0,f)\leqslant \rho _{\Psi ,\varphi }(f)$ . It remains to prove that (iii) implies (i).

Let $f_1,\ldots ,f_k$ be linearly independent solutions of (2-1), and let $y_1,\ldots ,y_{k-1}$ be defined by (6-1). Let $j\in \{1,\ldots ,k-1\}$ . We note that the zeros and poles of $y_j=f_j/f_k$ are sequences with $(\Psi ,\varphi )$ -exponent of convergence less than or equal to $\lambda $ by assumption (iii). The same is true for the 1-points of $y_j$ , as they are precisely the zeros of $f_j-f_k$ , which is also a solution of (2-1). In other words,

(6-12) $$ \begin{align} \max\{ \lambda_{\Psi,\varphi}(0,y_j),\lambda_{\Psi,\varphi}(\infty,y_j),\lambda_{\Psi,\varphi}(1,y_j) \} \leqslant \lambda. \end{align} $$

Suppose that $y_j(0)\neq 0,\infty ,1$ and $y_j'(0)\neq 0$ . By the second main theorem of Nevanlinna [20, Theorem 1.4] and the Gol’dberg–Grinshtein estimate [2, Corollary 3.2.3], we now have

(6-13) $$ \begin{align} \begin{aligned} T(r,y_j) & \leqslant N(r,y_j,0)+N(r,y_j,\infty)+N(r,y_j,1)\\ &\quad +O\bigg(1+\log^+\frac{s(r)}{r(s(r)-r)}+\log^+T(s(r),y_j)\bigg). \end{aligned} \end{align} $$

Since $\rho _{\Psi ,\varphi }(f)<\infty $ for all solutions f of (2-1), we deduce $\rho _{\Psi ,\varphi }(y_j)<\infty $ . In fact, we prove

(6-14) $$ \begin{align} \rho_{\Psi,\varphi}(y_j)\leqslant \lambda,\quad j=1,\ldots,k-1. \end{align} $$

Clearly we may suppose that $T(r,y_j)$ is an unbounded function of r. Since

$$ \begin{align*} \begin{aligned} \frac{\Psi( \log\log \, T(s(r),y_j))}{\log\varphi(r)} & = o \bigg( \frac{\Psi( \log \, T(s(r),y_j))}{\log\varphi(s(r))} \cdot \frac{\log\varphi(s(r))}{\log\varphi(r)} \bigg) = o(1), \end{aligned} \end{align*} $$

as $r\to \infty $ , assertion (6-14) follows by (2-8) (or (2-6)), (6-12) and (6-13). If $y_j(0)\in \{0,\infty ,1\}$ or $y_j'(0)=0$ , then assertion (6-14) follows by standard arguments and the fact that rational functions are of $(\Psi ,\varphi )$ -order zero by the assumption $\rho _{\Psi ,\varphi }(\log ^+ r)=0$ .

It is claimed in [12, page 719] that the functions $1,y_1,\ldots , y_{k-1}$ are linearly independent meromorphic solutions of the differential equation

$$ \begin{align*} y^{(k)}-\frac{W_{k-1}(z)}{W_k(z)}y^{(k-1)}+\cdots + (-1)^{k+1}\frac{W_1(z)}{W_k(z)}y'=0, \end{align*} $$

where the functions $W_j$ are defined by (6-2). This can be verified by restating [13, Proposition 1.4.7] with the aid of some basic properties satisfied by Wronskian determinants [13, Ch. 1.4]. From Lemma 6.2 we now conclude

$$ \begin{align*} \int_{D(0,r)}\bigg|\frac{W_i(z)}{W_k(z)}\bigg|^{{1}/({k-i})} dm(z) \lesssim s(r) \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant k-1} T(s(r),y_l) ) \end{align*} $$

for all $i=1,\ldots , k-1$ , or, in other words,

(6-15) $$ \begin{align} \int_{D(0,r)}\bigg|\frac{W_{k-i}(z)}{W_k(z)}\bigg|^{{1}/{i}} dm(z) \lesssim s(r) \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant k-1} T(s(r),y_l) ) \end{align} $$

for all $i=1,\ldots , k-1$ . By (2-4), (2-7), (6-2) and (6-14) it is clear that $\rho _{\Psi ,\varphi }(W_k)\leqslant \lambda $ . Since $\sqrt [k]{W_k}$ is a well-defined meromorphic function in $D(0,R)$ by (6-4), it follows that $\rho _{\Psi ,\varphi }(\sqrt [k]{W_k})\leqslant \lambda $ . By Corollary 3.4, we have

(6-16) $$ \begin{align} & \int_{D(0,r)}\bigg|\frac{(\sqrt[k]{W_k})^{(k-i-j)}(z)}{\sqrt[k]{W_k}(z)}\bigg|^{{1}/({k-i-j})} \, dm(z)\nonumber\\ & \quad \lesssim s(r) \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant k-1} T(s(r),y_l) ), \end{align} $$

where i and j are as in (6-3). From (6-3), we deduce

$$ \begin{align*} |A_j|^{{1}/({k-j})}\lesssim \bigg|\frac{(\sqrt[k]{W_k})^{(k-j)}}{\sqrt[k]{W_k}}\bigg|^{{1}/({k-j})} +\sum_{i=1}^{k-j}\bigg|\frac{W_{k-i}}{W_k}\bigg|^{{1}/({k-j})} \bigg|\frac{(\sqrt[k]{W_k})^{(k-i-j)}}{\sqrt[k]{W_k}}\bigg|^{{1}/({k-j})}. \end{align*} $$

Finally, we make use of Hölder’s inequality with conjugate indices $p=(k-j)/i$ and $q=(k-j)/(k-i-j)$ , $1\leqslant i< k-j$ ( $i=k-j$ is a removable triviality), together with (6-15) and (6-16), and conclude

$$ \begin{align*} \frac{1}{r} \int_{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z) \lesssim \frac{s(r)}{r} \log\frac{e\, s(r)}{s(r)-r} ( S(r)+ \max_{1\leqslant l\leqslant k-1} T(s(r),y_l) ) \end{align*} $$

for $j=0,\ldots ,k-1$ . By (2-8), (6-14) and the properties of $\Psi $ and $\varphi $ , we deduce

$$ \begin{align*}\rho_{\Psi,\varphi}\bigg(\frac{1}{r} \int_{D(0,r)}|A_j(z)|^{{1}/({k-j})}\, dm(z)\bigg)\leqslant\lambda, \quad j=0,\ldots,k-1.\end{align*} $$

We have proved that (i), (ii), (iii) are equivalent. A similar proof applies for strict inequalities.

7 Proof of Theorem 2.1

Note that the assumption $\Psi (x^2)\lesssim \Psi (x)$ , $0\leqslant x < \infty $ , implies

$$ \begin{align*} \Psi(xy) \lesssim \Psi(x) + \Psi(y), \quad \Psi(x + y) \lesssim \Psi(x) + \Psi(y) + 1 \end{align*} $$

for all $0\leqslant x,y <\infty $ . The following result is a counterpart of Lemma 6.2.

Lemma 7.1. Suppose that $\Psi , s,\omega $ are functions as in Theorem 2.1. Let $g_1,\ldots , g_k$ be linearly independent meromorphic solutions of a linear differential equation (6-5) with coefficients $B_0,\ldots ,B_{k-1}$ meromorphic in $D(0,R)$ . If

$$ \begin{align*} \int_0^R \Psi( T(r,g_j) ) \, \omega(r) \, dr < \infty, \quad j=0,\dotsc,k, \end{align*} $$

then

$$ \begin{align*} \int_0^R \Psi\bigg( \int_{D(0,r)} |B_j(z)|^{{1}/({k-j})} \, dm(z) \bigg) \, \omega(r)\, dr < \infty, \quad j=0,\dotsc,k-1. \end{align*} $$

Proof. We only consider a special case of (6-5), where all intermediate coefficients are identically zero, that is,

(7-1) $$ \begin{align} g^{(k)} + B_0 g = 0. \end{align} $$

The general case can be obtained by using the Frank–Hennekemper approach as in the proof of Lemma 6.2, or by applying the standard order reduction procedure [18, pages 106–107].

Let g be any nontrivial meromorphic solution of (7-1). Now

(7-2) $$ \begin{align} \int_r^R \Psi( T(t,g) ) \, \omega(t) \, dt \geqslant \Psi( T(r,g) ) \, \widehat{\omega}(r), \quad 0\leqslant r < R. \end{align} $$

Note that the left-hand side of (7-2) decays to zero as $r\to R^-$ . Corollary 3.4 implies

$$ \begin{align*} \begin{aligned} \int_{D(0,r)} \bigg| \frac{g^{(k)}(z)}{g(z)} \bigg|^{{1}/{k}} \, dm(z) & \lesssim s(r) \log\frac{e \, s(r)}{s(r)-r} \bigg( 1 + \log^+\!\frac{s(r)}{r(s(r)-r)} + T(s(r),g ) \bigg) \end{aligned} \end{align*} $$

for all $0<r<R$ . Therefore, by the properties of $\Psi $ , we obtain

(7-3) $$ \begin{align} & \int_0^R \Psi\bigg( \int_{D(0,r)} |B_0(z)|^{{1}/{k}} \, dm(z) \bigg) \, \omega(r) \, dr\notag\\ & \quad \lesssim \int_0^R \Psi( T(s(r),g) ) \, \omega(r) \, dr + \int_0^R \Psi\bigg( s(r) \log\frac{e \, s(r)}{s(r)-r} \bigg) \, \omega(r) \, dr +1. \end{align} $$

The latter integral in (7-3) is finite by (2-2), while the former integral is integrated by parts as follows:

$$ \begin{align*} & \int_0^R \Psi( T(s(r),g) ) \, \omega(r) \, dr = \int_{s(0)}^R \Psi( T(t,g) ) \, \omega(s^{-1}(t) ) \, (s^{-1})'(t) \, dt \\ & \quad = -\Psi( T(s(0),g) ) \bigg( - \int_{s(0)}^R \omega(s^{-1}(x) ) \, (s^{-1})'(x) \, dx \bigg) \\ &\quad \quad - \int_{s(0)}^R \bigg( \frac{\partial}{\partial t} \Psi( T(t,g) ) \bigg) \bigg( - \int_t^R \omega(s^{-1}(x) ) \, (s^{-1})'(x) \, dx \bigg)\, dt \\ & \quad = \Psi( T(s(0),g) ) \, \widehat{\omega}(0) + \int_{s(0)}^R \bigg( \frac{\partial}{\partial t} \Psi( T(t,g) ) \bigg) \widehat{\omega}(s^{-1}(t)) \, dt. \end{align*} $$

By using the assumption on $\widehat {\omega }$ and integrating by parts again, we deduce

$$ \begin{align*} & \int_0^R \Psi( T(s(r),g) ) \, \omega(r) \, dr\\ & \quad \lesssim \Psi( T(s(0),g) ) \, \widehat{\omega}(0) + \int_{s(0)}^R \bigg( \frac{\partial}{\partial t} \Psi( T(t,g) ) \bigg) \widehat{\omega}(t) \, dt \\ & \quad \lesssim \Psi( T(s(0),g) ) \, \widehat{\omega}(0) + \lim_{t\to R^-} \!\!\bigg( \!\Psi( T(t,g) ) \, \widehat{\omega}(t) \!\bigg) + \int_{s(0)}^R \!\Psi( T(t,g) ) \, \omega(t) \, dt \\ & \quad \lesssim \Psi( T(s(0),g) ) \, \frac{\widehat{\omega}(0)}{\widehat{\omega}(s(0))} \int_{s(0)}^R \omega(t)\, dt + \int_{s(0)}^R \Psi( T(t,g) ) \, \omega(t) \, dt \\ & \quad \lesssim \bigg( \frac{\widehat{\omega}(0)}{\widehat{\omega}(s(0))} + 1\bigg) \int_{s(0)}^R \Psi( T(t,g) ) \, \omega(t) \, dt < \infty. \end{align*} $$

The assertion follows.

Proof of Theorem 2.1.

Assume that (i) holds, and let f be any solution of (2-1). By (6-11), there exists a constant $C=C(f)>0$ such that

$$ \begin{align*} \int_0^R \Psi( T(r,f) ) \, \omega(r) \, dr \leqslant \int_0^R \Psi\bigg( \frac{C}{r} \sum_{j=0}^{k-2} \int_{D(0,r)} |A_j(z)|^{{1}/({k-j})} \, dm(z) + C \bigg) \, \omega(r) \, dr. \end{align*} $$

We deduce (ii) by the properties of $\Psi $ .

Since (ii) trivially implies (iii), we only need to prove that (iii) implies (i). A similar argument appears in the proof of Theorem 2.4, and therefore we only sketch the proof. Let $f_1,\dotsc ,f_k$ be linearly independent solutions of (2-1), and define $y_j = f_j/f_k$ for ${j=1,\dotsc ,k}$ .

Integrating by parts as in the proof of Lemma 7.1, and using $\Psi (\log x) = o(\Psi (x))$ , we deduce for each $\varepsilon>0$ the existence of $r_0\in (0,R)$ such that

$$ \begin{align*} \int_{r_0}^{R_0} \Psi( \log T(s(r),y_j) )\, \omega(r)\, dr \leqslant \varepsilon \int_{r_0}^{R_0} \Psi(T(r,y_j) )\, \omega(r)\, dr \end{align*} $$

for all $R_0\in (r_0,R)$ . By applying the second main theorem of Nevanlinna (6-13), choosing an appropriate $\varepsilon>0$ and reorganizing terms, we obtain

$$ \begin{align*} \begin{aligned} \int_{r_0}^{R_0} \Psi(T(r,y_j)) \, \omega(r)\, dr\lesssim\ & \max_{\zeta\in\{0,\infty,1\}}\int_{r_0}^{R_0} \Psi(N(r,y_j,\zeta))\, \omega(r)\, dr +1. \end{aligned} \end{align*} $$

By letting $R_0\to R$ , and applying (iii), we deduce

$$ \begin{align*} \int_0^R \Psi( T(r,y_j) ) \, \omega(r) \, dr < \infty, \quad j=1, \dotsc,k. \end{align*} $$

The condition (i) can be deduced from Lemma 7.1 by an argument similar to that in the proof of Theorem 2.4. With this guidance, we consider Theorem 2.1 proved.

8 Proof of Theorem 2.3

The proof is similar to that of [16, Theorem 7.9]. We content ourselves with proving the following result, which plays a crucial role in the reasoning yielding Theorem 2.3. More precisely, it is a counterpart of [16, Lemma 7.7].

Lemma 8.1. Let $\omega \in \mathcal {D}$ , and let $k>j\geqslant 0$ be integers. If f is a meromorphic function in $\mathbb {D}$ such that $\int _0^1 T(r,f) \, \omega (r)\, dr<\infty $ , then

$$ \begin{align*} \int_{\mathbb{D}} \, \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})}\, \widehat{\omega}(z)\, dm(z) < \infty. \end{align*} $$

Proof. Let $\{\varrho _n\}$ be a sequence of points in $(0,1)$ such that $\varrho _0=0$ and $\widehat {\omega }(\varrho _n)=\widehat {\omega }(0)/K^n$ for $n\in \mathbb {N}$ . By [15, Lemma 2.1], the assumption $\omega \in \widehat {\mathcal {D}}$ is equivalent to the fact that there exist constants $K=K(\omega )>1$ and $C=C(\omega ,K)>1$ such that $1-\varrho _n \geqslant C (1-\varrho _{n+1})$ for all $n\in \mathbb {N}$ . Let K be fixed in such a way. The assumption is equivalent to the fact that there exists a constant $\mu =\mu (\omega ,K)>1$ such that $1-\varrho _n \leqslant \mu (1-\varrho _{n+1})$ for all $n\in \mathbb {N}$ ; see, for example, the beginning of the proof of [17, Theorem 7]. These properties give

$$ \begin{align*} \frac{\varrho_{n+2}-\varrho_n}{\varrho_{n+2}-\varrho_{n+1}} = \frac{(1-\varrho_n) - (1-\varrho_{n+2})}{(1-\varrho_{n+1})-(1-\varrho_{n+2})} \leqslant \frac{\mu -1/\mu}{1-1/C}, \quad n\in\mathbb{N}. \end{align*} $$

Then, by Corollary 3.4, we obtain

$$ \begin{align*} & \int_{\mathbb{D}} \, \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})} \, \widehat{\omega}(z)\, dm(z)\\ & \quad \leqslant \sum_{n=0}^\infty \, \widehat{\omega}(\varrho_n) \int_{\varrho_{n}\leqslant |z| < \varrho_{n+1}} \bigg| \frac{f^{(k)}(z)}{f^{(\kern1.2pt j)}(z)} \bigg|^{{1}/({k-j})} \, dm(z)\\ & \quad \lesssim \sum_{n=0}^\infty \, \widehat{\omega}(\varrho_n) \, \bigg( 1 + \log\frac{1}{\varrho_{n+2}-\varrho_{n+1}} + T(\varrho_{n+2}, f) \bigg) =: S_1 + S_2 + S_3. \end{align*} $$

We consider these sums separately. Now $S_1= \widehat {\omega }(0) \, \sum _{n=0}^\infty K^{-n}<\infty $ , while

$$ \begin{align*} S_2 & \leqslant \bigg( \log \frac{C}{C-1} \bigg) \, \sum_{n=0}^\infty \widehat{\omega}(\varrho_n) + \frac{K^2}{K-1} \sum_{n=0}^\infty \log\frac{1}{1-\varrho_{n+1}} \int_{\varrho_{n+1}}^{\varrho_{n+2}} \omega(s) \, ds\\ & \lesssim 1 + \int_{\varrho_1}^1 \log\frac{1}{1-s} \, \omega(s) \, ds. \end{align*} $$

To see that this last integral is finite, let $r_n=1-2^{-n}$ for $n\in \mathbb {N}\cup \{0\}$ , and compute

$$ \begin{align*} \int_0^1 \log\frac{1}{1-s} \, \omega(s) \, ds & \leqslant \sum_{n=0}^\infty \log\frac{1}{1-r_{n+1}} \, ( \widehat{\omega}(r_n) - \widehat{\omega}(r_{n+1})) \\ & \lesssim \sum_{n=1}^\infty n \, \widehat{\omega}(r_n) \lesssim \sum_{n=1}^\infty \frac{n}{K^n} < \infty. \end{align*} $$

Finally, we estimate $S_3$ by

$$ \begin{align*} S_3 & \leqslant \frac{K^3}{K-1} \, \sum_{n=0}^\infty \int_{\varrho_{n+2}}^{\varrho_{n+3}} T(r, f) \, \omega(r)\, dr \leqslant \frac{K^3}{K-1} \, \int_{\varrho_{2}}^{1} T(r, f) \, \omega(r)\, dr < \infty. \end{align*} $$

This completes the proof of Lemma 8.1.

Lemma 8.1 fails to be true if the hypothesis $\omega \in \mathcal {D}$ is replaced with $\omega \in \widehat {\mathcal {D}}$ . To see this, it suffices to consider the function

$$ \begin{align*} f(z) = \exp\bigg( \frac{\log(1/(1-z))}{1-z}\bigg), \quad z\in\mathbb{D}, \end{align*} $$

which satisfies $T(r,f) \asymp \log (1/(1-r))$ as $r\to 1^-$ by [4, Example 3], and the weight

$$ \begin{align*} \omega(r) = \frac{1}{(1-r)\bigg( \log\dfrac{e}{1-r} \bigg)^\alpha}, \quad 0\leqslant r<1, \end{align*} $$

which belongs to $\widehat {\mathcal {D}}$ for any $\alpha>1$ . If $\alpha>2$ , then $\int _0^1 T(r,f) \, \omega (r)\, dr<\infty $ . However, the integral

(8-1) $$ \begin{align} \int_{\mathbb{D}} \bigg| \frac{f'(z)}{f(z)} \bigg| \widehat{\omega}(z) \, dm(z) \asymp \int_{\mathbb{D}} \frac{1}{|1-z|^2} \bigg|1+\log\frac{1}{1-z} \bigg| \bigg( \log\frac{e}{1-|z|} \bigg)^{1-\alpha} \, dm(z) \end{align} $$

diverges for $\alpha \leqslant 3$ . If (8-1) is computed using polar coordinates, then the integral with respect to the argument can be computed similarly to [4, page 174].