Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-12T19:44:51.144Z Has data issue: false hasContentIssue false
  • English
  • Français

DERIVATION RELATION FOR FINITE MULTIPLE ZETA VALUES IN 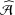$\widehat{{\mathcal{A}}}$

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  08 January 2020

HIDEKI MURAHARA Open the ORCID record for HIDEKI MURAHARA [Opens in a new window]  and
TOMOKAZU ONOZUKA
HIDEKI MURAHARA
Affiliation:
Nakamura Gakuen University Graduate School, 5-7-1, Befu, Jonan-ku, Fukuoka, 814-0198, Japan e-mail: [email protected]
TOMOKAZU ONOZUKA*
Affiliation:
Multiple Zeta Research Center, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka, 819-0395, Japan
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Ihara et al. proved the derivation relation for multiple zeta values. The first-named author obtained its counterpart for finite multiple zeta values in 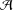${\mathcal{A}}$. In this paper, we present its generalization in 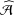$\widehat{{\mathcal{A}}}$.

Keywords

multiple zeta valuesfinite multiple zeta valuesderivation relation

MSC classification

Primary: 11M32: Multiple Dirichlet series and zeta functions and multizeta values
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 2 , April 2021 , pp. 260 - 265
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Coons

References

Hoffman, M. E., ‘Multiple harmonic series’, Pacific J. Math. 152 (1992), 275–290.Google Scholar
Hoffman, M. E., ‘The algebra of multiple harmonic series’, J. Algebra 194 (1997), 477–495.Google Scholar
Hoffman, M. E., ‘Quasi-symmetric functions and mod p multiple harmonic sums’, Kyushu J. Math. 69 (2015), 345–366.Google Scholar
Horikawa, Y., Oyama, K. and Murahara, H., ‘A note on derivation relations for multiple zeta values and finite multiple zeta values’, Preprint, 2018, arXiv:1809.08389.Google Scholar
Ihara, K., Kaneko, M. and Zagier, D., ‘Derivation and double shuffle relations for multiple zeta values’, Compos. Math. 142 (2006), 307–338.Google Scholar
Jarossay, D., ‘An explicit theory of $\unicode[STIX]{x1D70B}^{\text{un,crys}}(\mathbb{P}^{1}-\{0,\unicode[STIX]{x1D707}_{N},\infty \})$’, Preprint, 2014, arXiv:1412.5099.Google Scholar
Murahara, H., ‘Derivation relations for finite multiple zeta values’, Int. J. Number Theory 13 (2017), 419–427.Google Scholar
Rosen, J., ‘Asymptotic relations for truncated multiple zeta values’, J. Lond. Math. Soc. (2) 91 (2015), 554–572.Google Scholar
Seki, S., ‘Finite multiple polylogarithms’, Doctoral Dissertation, Osaka University, 2017.Google Scholar
Seki, S., ‘The p -adic duality for the finite star-multiple polylogarithms’, Tohoku Math. J. (2) 71 (2019), 111–122.Google Scholar