Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T19:11:23.681Z Has data issue: false hasContentIssue false
  • English
  • Français

Cubature method for the numerical solution of the characteristic initial value problem

uxy = f(x, y, u, ux, Uy)

Published online by Cambridge University Press:  09 April 2009

M. K. Jain  and
K. D. Sharma
M. K. Jain
Affiliation:
Department of MathematicsIndian Institute of TechnologyHauz Khas, New Delhi-29India
K. D. Sharma
Affiliation:
Department of MathematicsIndian Institute of TechnologyHauz Khas, New Delhi-29India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

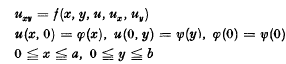The resemblance of the Goursat problem for the hyperbolic partial differential equations to the initial value problem 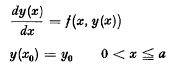for the ordinary differential equations has suggested the extension of many well known numerical methods existing for (1.2) to the numerical treatment of (1.1). Day [2] discusses the quadrature methods while Diaz [3] generalizes the simple Euler-method. Moore [6] gives an analogue to the fourth order Runge-Kutta-method and Tornig [7] generalizes the explicit and implicit Adams-methods.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 2 , May 1968 , pp. 355 - 368
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Butcher, J. C., ‘A modified multistep method for the numerical integration of ordinary differential equations’, J. ACM 12 (1960), 124–135.CrossRefGoogle Scholar
[2]Day, J. T., ‘A Gaussian quadrature methods for the numerical solution of the characteristic initial value problem uxv = f(x, y, u)’ Math. Comp. 17 (1963), 438–441.Google Scholar
[3]Diaz, J., ‘On an analogue of the Euler-Cauchy polygon method for the numerical solution of uxy = f(x, y, u, ux, uy)’ Arch. Rat. Mech. Anal. 1 (1957). 154–180.CrossRefGoogle Scholar
[4]Jordan, C.. Cours d'Analyses (Gauthier-Villars, Paris, Third Edition, V. 3, 1915, p. 369–371).Google Scholar
[5]Henrici, P., Discrete variable methods in ordinary differential equation (Wiley U. Sons, 1962).Google Scholar
[6]Moore, R. H., ‘A Runge-Kutta procedure for the Goursat problem in hyperbolic partial differential equations’, Arch. Rat. Mech. Anal. 7 (1961), 37–63.CrossRefGoogle Scholar
[7]Töring, W., ‘Zur numerischen Behandlung von Anfangswert problemen partieller hyperbolischer Differentialgleichungen Zweiter Ordung in Zwei Unabhängigen Veränderlichen’, Arch. Rat. Mech. Anal. 4, (1960), 428–466.CrossRefGoogle Scholar
[8]Tyler, G. W., ‘Numerical integration of functions of several variables, Canad. J. Math., Vol. 5 (1953), 393–412.CrossRefGoogle Scholar