Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barnes, E. S.
and
Wall, G. E.
1959.
Some extreme forms defined in terms of Abelian groups.
Journal of the Australian Mathematical Society,
Vol. 1,
Issue. 1,
p.
47.
1969.
Geometry of Numbers.
p.
471.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Bergé, Anne-Marie
and
Martinet, Jacques
1989.
Sur un problème de dualité lié aux sphères en géométrie des nombres.
Journal of Number Theory,
Vol. 32,
Issue. 1,
p.
14.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Gruber, Peter M.
2016.
Application of an idea of Voronoĭ to lattice packing, supplement.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 195,
Issue. 2,
p.
473.


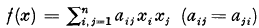 , of determinant
, of determinant 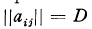 and minimum M for integral
and minimum M for integral 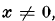 , is said to be extreme if the ratio
, is said to be extreme if the ratio 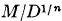 is a (local) maximum for small variations in the coefficients
is a (local) maximum for small variations in the coefficients 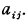 .
.