Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T16:56:25.106Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONVOLUTION-INDUCED TOPOLOGY ON THE ORLICZ SPACE OF A LOCALLY COMPACT GROUP

Part of: Abstract harmonic analysis Topological linear spaces and related structures Linear function spaces and their duals

Published online by Cambridge University Press:  19 January 2015

IBRAHIM AKBARBAGLU  and
SAEID MAGHSOUDI
IBRAHIM AKBARBAGLU
Affiliation:
Department of Mathematics, Faculty of Basic Sciences, University of Bonab, Bonab 55517-61167, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email [email protected]
SAEID MAGHSOUDI*
Affiliation:
Department of Mathematics, University of Zanjan, Zanjan 45195-313, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 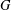$G$ be a locally compact group with a fixed left Haar measure. In this paper, given a strictly positive Young function 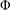${\rm\Phi}$, we consider 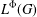$L^{{\rm\Phi}}(G)$ as a Banach left 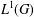$L^{1}(G)$-module. Then we equip 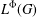$L^{{\rm\Phi}}(G)$ with the strict topology induced by 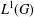$L^{1}(G)$ in the sense of Sentilles and Taylor. Some properties of this locally convex topology and a comparison with weak$^{\ast }$, bounded weak$^{\ast }$ and norm topologies are presented.

Keywords

Orlicz spacelocally compact groupconvolutionstrict topologybounded weak∗ topology

MSC classification

Primary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Secondary: 46A70: Saks spaces and their duals (strict topologies, mixed topologies, two-norm spaces, co-Saks spaces, etc.) 46A03: General theory of locally convex spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 1 , August 2015 , pp. 1 - 11
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Akbarbaglu, I. and Maghsoudi, S., ‘On certain porous sets in the Orlicz space of a locally compact group’, Colloq. Math. 129 (2012), 99–111.CrossRefGoogle Scholar
Akbarbaglu, I. and Maghsoudi, S., ‘Banach–Orlicz algebras on a locally compact group’, Mediterr. J. Math. 10 (2013), 1937–1947.CrossRefGoogle Scholar
Akbarbaglu, I., Maghsoudi, S. and Seoane-Sepúlveda, J. B., ‘A strict topology on Orlicz spaces’, Math. Nachr. doi:10.1002/mana.201400100.CrossRefGoogle Scholar
Bund, I. M., ‘Birnbaum–Orlicz spaces of functions on groups’, Pacific J. Math. 58 (1975), 351–359.CrossRefGoogle Scholar
Crombez, G. and Govaerts, W., ‘The convolution-induced topology on L ∞(G) and linearly dependent translates in L 1(G)’, Int. J. Math. Math. Sci. 5 (1982), 11–20.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T., Linear operators, Part I (Interscience Publishers, New York, 1958).Google Scholar
Feledziak, K. and Nowak, M., ‘Locally solid topologies on vector valued function spaces’, Collect. Math. 48 (1997), 487–511.Google Scholar
Grosser, M., Bidualräume und Vervollständigungen von Banachmoduln, Lecture Notes in Mathematics, 717 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, I, II (Springer, New York, 1975).Google Scholar
Hudzik, H., Kamińska, A. and Musielak, J., ‘On some Banach algebras given by a modular’, in: Alfred Haar Memorial Conference, Budapest, Colloq. Math. Soc. János. Bolyai, 49 (North-Holland, Amsterdam, 1987), 445–463.Google Scholar
Josefson, B., ‘Weak sequential convergence in the dual of a Banach space does not imply norm convergence’, Ark. Mat. 13 (1975), 79–89.CrossRefGoogle Scholar
Kamińska, A. and Musielak, J., ‘On convolution operator in Orlicz spaces’, Rev. Mat. Complut. 2 (1989), 157–178.CrossRefGoogle Scholar
Khan, L. A., Function Spaces, Contemporary Mathematics, 435 (ed. Jarosz, K.) (American Mathematical Society, Providence, RI, 2007), 253–263.CrossRefGoogle Scholar
Khan, L. A., ‘Topological modules of continuous homomorphisms’, J. Math. Anal. Appl. 343 (2008), 141–150.CrossRefGoogle Scholar
Khan, L. A., Mohammad, N. and Thaheem, A. B., ‘The strict topology on topological algebras’, Demonstratio Math. 38 (2005), 883–894.CrossRefGoogle Scholar
Krasnosel’skii, M. A. and Rutickii, Ya. B., Convex Functions and Orlicz Spaces (Noordhoff, Groningen, 1961).Google Scholar
Maghsoudi, S., ‘The space of vector-valued integrable functions under certain locally convex topologies’, Math. Nachr. 286 (2013), 260–271.CrossRefGoogle Scholar
Nissenzweig, A., ‘W ∗ sequential convergence’, Israel J. Math. 22 (1975), 266–272.CrossRefGoogle Scholar
Nowak, M., ‘On some linear topology on Orlicz spaces L E∗𝜑(𝜇). I’, Ann. Soc. Math. Pol., Ser. I, Comment. Math. 26 (1986), 51–68.Google Scholar
Nowak, M., ‘On the modular topology on Orlicz spaces’, Bull. Pol. Acad. Sci. Math. 36 (1988), 553–562.Google Scholar
Nowak, M., ‘A generalized mixed topology on Orlicz spaces’, Rev. Mat. Complut. 7 (1994), 27–56.CrossRefGoogle Scholar
Rao, M. M. and Ren, Z. D., Theory of Orlicz Spaces (Marcel Dekker, New York, 1991).Google Scholar
Rubel, L. A. and Ryff, J. V., ‘The bounded weak-star topology and the bounded analytic functions’, J. Funct. Anal. 5 (1970), 167–183.CrossRefGoogle Scholar
Sentilles, F. D. and Taylor, D., ‘Factorization in Banach algebras and the general strict topology’, Trans. Amer. Math. Soc. 142 (1969), 141–152.CrossRefGoogle Scholar
Shantha, K. V., ‘The general strict topology in locally convex modules over locally convex algebras I’, Ital. J. Pure Appl. Math. 16 (2004), 211–226.Google Scholar
Shantha, K. V., ‘The general strict topology in locally convex modules over locally convex algebras II’, Ital. J. Pure Appl. Math. 17 (2005), 21–32.Google Scholar
Shapiro, J. H., ‘The bounded weak star topology and the general strict topology’, J. Funct. Anal. 8 (1971), 272–286.CrossRefGoogle Scholar
Singh, A. I., ‘L 0∞(G)∗ as the second dual of the group algebra L 1(G) with a locally convex topology’, Michigan Math. J. 46 (1999), 143–150.CrossRefGoogle Scholar
Yap, L. Y. H., ‘On the ranges of certain convolution operators’, Expo. Math. 11 (1993), 73–80.Google Scholar