No CrossRef data available.
Article contents
A convolution semigroup of modular functions
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let S be a compact topological semigroup, and let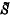 
be the collection of all normalized non-negative Borel measures on S. It is well-known that 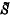, under convolution and the topology induced by the weak-star topology on the dual of the Benach space C(S) of all complex valued continuous functions on S, forms a compact topological semigroup which is known as the convolution semigroup of measures (see for instance, Glicksberg [3], Collins [1], Schwarz [5] and the author [4]). [1], Schwarz [5] and the author [4]). Professor A. D. Wallace asked if the process of forming the convolution semigroup of measures might be generalized to a more general class of set functions, the so-called “modular functions.” The purpose of the present note is to settle this question in the affirmative under a slight restriction. Before we are able to state the Wallace problem precisely, some preliminaries are necessary.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1966
References
[1]Collins, H. B., ‘The kernel of a semigroup of measures’, Duke Math. J., 28 (1961) 381–392.CrossRefGoogle Scholar
[2]Dunford, N. and Schwartz, J. T., Linear operations I, Interscience Publishers, New York (1958).Google Scholar
[3]Glicksberg, I., ‘Convolution semigroups of measures’, Pacific J. Math., 9 (1959), 51–67.CrossRefGoogle Scholar
[4]Lin, Y.-F., ‘Not necessarily Abelian convolution semigroups of probability measure’, Math. Z., 91 (1966), 300–307.CrossRefGoogle Scholar
[5]Schwarz, S., ‘Probability measures on non-commutative semigroups’, Proc. Symp. in General Topology and its Relations to Modern Analysis and Algebra, Prague (1962).Google Scholar
You have
Access