Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T01:36:47.126Z Has data issue: false hasContentIssue false
  • English
  • Français

CONFORMALLY FLAT CONTACT THREE-MANIFOLDS

Part of: Symplectic geometry, contact geometry Global differential geometry

Published online by Cambridge University Press:  03 November 2016

JONG TAEK CHO  and
DONG-HEE YANG
JONG TAEK CHO*
Affiliation:
Department of Mathematics, Chonnam National University, Gwangju 61186, Korea email [email protected]
DONG-HEE YANG
Affiliation:
Department of Mathematics and Statistics, Graduate School of Chonnam National University, Gwangju 61186, Korea email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider contact metric three-manifolds 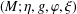$(M;\unicode[STIX]{x1D702},g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D709})$ which satisfy the condition 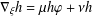$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}h=\unicode[STIX]{x1D707}h\unicode[STIX]{x1D711}+\unicode[STIX]{x1D708}h$ for some smooth functions 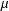$\unicode[STIX]{x1D707}$ and $\unicode[STIX]{x1D708}$, where 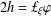$2h=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}$. We prove that if 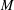$M$ is conformally flat and if 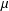$\unicode[STIX]{x1D707}$ is constant, then 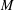$M$ is either a flat manifold or a Sasakian manifold of constant curvature 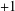$+1$. We cannot extend this result for a smooth function 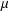$\unicode[STIX]{x1D707}$. Indeed, we give such an example of a conformally flat contact three-manifold which is not of constant curvature.

Keywords

contact three-manifoldsconformally flat metrics

MSC classification

Primary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.)
Secondary: 53D10: Contact manifolds, general
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 177 - 189
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2014R1A1A2053665).

References

Bang, K. and Blair, D. E., ‘The Schouten tensor and conformally flat manifolds’, in: Topics in Differential Geometry (Editura Academiei Romane, Bucharest, 2008), 1–28.Google Scholar
Blair, D. E., Riemannian Geometry of Contact and Symplectic Manifolds, 2nd edn, Progress in Mathematics, 203 (Birkhäuser, Boston, MA, 2010).Google Scholar
Calvaruso, G., ‘Einstein-like and conformally flat contact metric three-manifolds’, Balkan J. Geom. Appl. 5 (2000), 17–36.Google Scholar
Calvaruso, G., Perrone, D. and Vanhecke, L., ‘Homogeneity on three-dimensional contact metric manifolds’, Israel J. Math. 114 (1999), 301–321.Google Scholar
Cho, J. T. and Inoguchi, J., ‘Characteristic Jacobi operator on contact Riemannian 3-manifolds’, Differ. Geom. Dyn. Syst. 17 (2015), 49–71.Google Scholar
Cho, J. T. and Lee, J-E., ‘𝜂-parallel contact 3-manifolds’, Bull. Korean Math. Soc. 45 (2003), 475–492.Google Scholar
Ghosh, A. and Sharma, R., ‘A generalization of K-contact and (𝜅, 𝜇)-contact manifolds’, J. Geom. 103 (2013), 431–443.Google Scholar
Gouli-Andreou, F. and Tsolakidou, N., ‘On conformally flat contact metric manifolds with Q𝜉 =𝜌𝜉’, Beitr. Algebra Geom. 45 (2004), 103–115.Google Scholar
Koufogiorgos, T., Markellos, M. and Papantoniou, J., ‘The harmononicity of the Reeb vector field on contact metric 3-manifolds’, Pacific J. Math. 234 (2008), 325–344.Google Scholar
Okumura, M., ‘Some remarks on space with a certain structure’, Tôhoku Math. J. (2) 14 (1962), 135–145.Google Scholar
Perrone, D., ‘Weakly 𝜑-symmetric contact metric spaces’, Balkan J. Geom. Appl. 7 (2002), 67–77.Google Scholar
Perrone, D., ‘Contact metric manifolds whose characteristic vector field is a harmonic vector field’, Differential Geom. Appl. 20 (2004), 367–378.Google Scholar
Tanno, S., ‘Locally symmetric K-contact Riemannian manifolds’, Proc. Japan Acad. 43 (1967), 581–583.Google Scholar