Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
459.
Wang, Yi
and
Yeh, Yeong-Nan
2005.
Polynomials with real zeros and Pólya frequency sequences.
Journal of Combinatorial Theory, Series A,
Vol. 109,
Issue. 1,
p.
63.


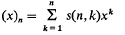
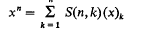
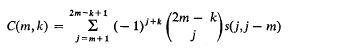
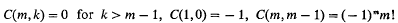 and
and 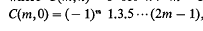 and
and 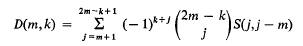
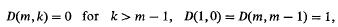 and
and 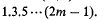 .
.