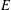Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T08:48:30.709Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLETE LATTICE HOMOMORPHISM OF STRONGLY REGULAR CONGRUENCES ON $E$-INVERSIVE SEMIGROUPS

Part of: Algebraic structures Semigroups

Published online by Cambridge University Press:  28 October 2015

XINGKUI FAN ,
QIANHUA CHEN  and
XIANGJUN KONG
XINGKUI FAN*
Affiliation:
School of Science, Qingdao University of Technology, Qingdao, Shandong 266520, PR China email [email protected]
QIANHUA CHEN
Affiliation:
School of Science, Qingdao University of Technology, Qingdao, Shandong 266520, PR China email [email protected]
XIANGJUN KONG
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu, Shandong 273165, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate strongly regular congruences on 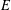$E$-inversive semigroups 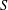$S$. We describe the complete lattice homomorphism of strongly regular congruences, which is a generalization of an open problem of Pastijn and Petrich for regular semigroups. An abstract characterization of left and right traces for strongly regular congruences is given. 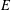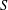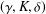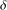The strongly regular (sr) congruences on $E$-inversive semigroups $S$ are described by means of certain strongly regular congruence triples $({\it\gamma},K,{\it\delta})$ consisting of certain sr-normal equivalences ${\it\gamma}$ and ${\it\delta}$ on 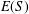$E(S)$ and a certain sr-normal subset 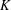$K$ of 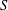$S$. Further, we prove that each strongly regular congruence on 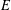$E$-inversive semigroups 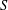$S$ is uniquely determined by its associated strongly regular congruence triple.

Keywords

E-inversive semigroupsstrongly regular congruenceleft tracecomplete lattice homomorphismstrongly regular congruence triple

MSC classification

Primary: 20M10: General structure theory
Secondary: 08A30: Subalgebras, congruence relations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 199 - 215
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Edwards, P. M., ‘Eventually regular semigroups’, Bull. Aust. Math. Soc. 28 (1983), 23–38.CrossRefGoogle Scholar
Fan, X. K. and Chen, Q. H., ‘Some characterizations of strongly regular congruences on E-inversive semigroups’, Adv. Math. (China) 42(4) (2013), 483–490.Google Scholar
Fan, X. K. and Chen, Q. H., ‘Strongly orthodox congruences on an E-inversive semigroup’, J. Aust. Math. Soc. 96 (2014), 216–230.CrossRefGoogle Scholar
Hayes, A., ‘E ∗ -dense E-semigroups’, Semigroup Forum 68 (2004), 218–232.CrossRefGoogle Scholar
Higgins, P. M., Techniques of Semigroup Theory (Oxford University Press, Oxford, 1992).CrossRefGoogle Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Clarendon Press, Oxford, 1995).CrossRefGoogle Scholar
Luo, Y. F. and Li, X. L., ‘𝓡-unipotent congruences on eventually regular semigroups’, Algebra Colloq. 14(1) (2007), 37–52.CrossRefGoogle Scholar
Luo, Y. F. and Li, X. L., ‘The maximum idempotent separating congruence on eventually regular semigroups’, Semigroup Forum 74 (2007), 306–318.CrossRefGoogle Scholar
Luo, Y. F. and Li, X. L., ‘Orthodox congruences on an eventually regular semigroup’, Semigroup Forum 74 (2007), 319–336.CrossRefGoogle Scholar
Luo, Y. F., Fan, X. K. and Li, X. L., ‘Regular congruences on an E-inversive semigroup’, Semigroup Forum 76 (2008), 107–123.CrossRefGoogle Scholar
Mitsch, H., ‘Subdirect products of E-inversive semigroups’, J. Aust. Math. Soc. 48 (1990), 66–78.Google Scholar
Mitsch, H. and Petrich, M., ‘Basic properties of E-inversive semigroups’, Comm. Algebra 28(11) (2000), 5169–5182.CrossRefGoogle Scholar
Pastijn, F. and Petrich, M., ‘Congruences on regular semigroups’, Trans. Amer. Math. Soc. 295 (1986), 607–633.CrossRefGoogle Scholar
Pastijn, F. and Petrich, M., ‘The congruence lattice of a regular semigroup’, J. Pure Appl. Algebra 53 (1988), 93–123.CrossRefGoogle Scholar
Thierrin, G., ‘Sur les demi-groupes inversés’, C. R. Acad. Sci. (Paris) 234 (1952), 1336–1338.Google Scholar
Trotter, P. G., ‘On a problem of Pastijn and Petrich’, Semigroup Forum 34 (1986), 249–252.CrossRefGoogle Scholar
Weipoltshammer, B., ‘Certain congruences on E-inversive E-semigroups’, Semigroup Forum 65 (2002), 233–248.CrossRefGoogle Scholar
Zheng, H. W., ‘Group congruences on an E-inversive semigroup’, Southeast Asian Bull. Math. 21 (1997), 1–8.Google Scholar