A coincidence problem in telephone traffic with non-recurrent arrival process

Extract

We consider the following problem. Calls arrive at a telephone exchange at the instants t₀, t₁, … t_m …. The telephone exchange contains a denumerable infinity of channels. The holding times of calls are non-negative random variables distributed independently of the times at which calls arrive, independently of which channel a call engages and independently of each other with a common distribution function B(x). Takacs [3Τ_m = t_m+1 − t_m, m ≧ are identically and independently distributed non-negative random variables with common distribution function, A (x). Finch [1] has studied the transient behaviour in the case of a recurrent arrival process and exponential holding time, that is when the common distribution of holding time is given by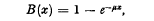 In this paper we make no assumption about the arrival process {t_m}. The underlying principle of this paper is the same as that of Finch [2]. We consider the instants of arrival t₀, t₁,…, t_m,… as given and determine various probabilities of interest conditionally as functions of the inter-arrival intervals Τ₁,…, Τ_m,… When the arrival process is a stochastic process we can then determine the relevant unconditional probabilities by integration.