Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-13T00:41:30.142Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CATENARY DEGREE OF KRULL MONOIDS II

Part of: Semigroups Algebraic number theory: global fields Sequences and sets Additive number theory; partitions General commutative ring theory

Published online by Cambridge University Press:  21 November 2014

ALFRED GEROLDINGER  and
QINGHAI ZHONG
ALFRED GEROLDINGER*
Affiliation:
University of Graz, NAWI Graz, Institute for Mathematics and Scientific Computing, Heinrichstraße 36, 8010 Graz, Austria email [email protected]
QINGHAI ZHONG
Affiliation:
University of Graz, NAWI Graz, Institute for Mathematics and Scientific Computing, Heinrichstraße 36, 8010 Graz, Austria email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 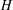$H$ be a Krull monoid with finite class group 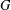$G$ such that every class contains a prime divisor (for example, a ring of integers in an algebraic number field or a holomorphy ring in an algebraic function field). 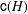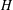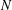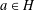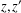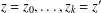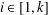The catenary degree $\mathsf{c}(H)$ of $H$ is the smallest integer $N$ with the following property: for each $a\in H$ and each pair of factorizations $z,z^{\prime }$ of $a$, there exist factorizations $z=z_{0},\dots ,z_{k}=z^{\prime }$ of $a$ such that, for each $i\in [1,k]$, 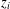$z_{i}$ arises from 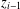$z_{i-1}$ by replacing at most 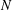$N$ atoms from 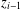$z_{i-1}$ by at most 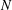$N$ new atoms. To exclude trivial cases, suppose that 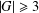$|G|\geq 3$. Then the catenary degree depends only on the class group 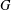$G$ and we have 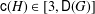$\mathsf{c}(H)\in [3,\mathsf{D}(G)]$, where 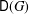$\mathsf{D}(G)$ denotes the Davenport constant of 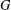$G$. The cases when 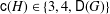$\mathsf{c}(H)\in \{3,4,\mathsf{D}(G)\}$ have been previously characterized (see Theorem A). Based on a characterization of the catenary degree determined in the paper by Geroldinger et al. [‘The catenary degree of Krull monoids I’, J. Théor. Nombres Bordeaux23 (2011), 137–169], we determine the class groups satisfying 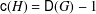$\mathsf{c}(H)=\mathsf{D}(G)-1$. Apart from the extremal cases mentioned, the precise value of 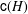$\mathsf{c}(H)$ is known for no further class groups.

Keywords

nonunique factorizationssets of lengthssets of distancescatenary degreeKrull monoidszero-sum sequences

MSC classification

Primary: 11R27: Units and factorization
Secondary: 11P70: Inverse problems of additive number theory, including sumsets 11B50: Sequences (mod $m$) 13A05: Divisibility; factorizations 20M13: Arithmetic theory of monoids
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 3 , June 2015 , pp. 324 - 354
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Bachman, D., Baeth, N. and Gossell, J., ‘Factorizations of upper triangular matrices’, Linear Algebra Appl. 450 (2014), 138–157.Google Scholar
Baeth, N. R. and Geroldinger, A., ‘Monoids of modules and arithmetic of direct-sum decompositions’, Pacific J. Math. 271 (2014), 257–319.CrossRefGoogle Scholar
Baeth, N. R., Ponomarenko, V., Adams, D., Ardila, R., Hannasch, D., Kosh, A., McCarthy, H. and Rosenbaum, R., ‘Number theory of matrix semigroups’, Linear Algebra Appl. 434 (2011), 694–711.CrossRefGoogle Scholar
Baeth, N. R. and Smertnig, D., Factorization theory in noncommutative settings, Preprint, 2014,arXiv:1402.4397.Google Scholar
Baeth, N. R. and Wiegand, R., ‘Factorization theory and decomposition of modules’, Amer. Math. Monthly 120 (2013), 3–34.Google Scholar
Baginski, P., Geroldinger, A., Grynkiewicz, D. J. and Philipp, A., ‘Products of two atoms in Krull monoids and arithmetical characterizations of class groups’, European J. Combin. 34 (2013), 1244–1268.Google Scholar
Chang, G. W. and Smertnig, D., ‘Factorization in the self-idealization of a PID’, Boll. Unione Mat. Ital. (9) 6(2) (2013), 363–377.Google Scholar
Chapman, S. T., Corrales, M., Miller, A., Miller, Ch. and Patel, Dh., ‘The catenary and tame degrees on a numerical monoid are eventually periodic’, J. Aust. Math. Soc. 97 (2014), 289–300.Google Scholar
Chapman, S. T., García-Sánchez, P. A. and Llena, D., ‘The catenary and tame degree of numerical monoids’, Forum Math. 21 (2009), 117–129.Google Scholar
Chapman, S. T., García-Sánchez, P. A., Llena, D., Ponomarenko, V. and Rosales, J. C., ‘The catenary and tame degree in finitely generated commutative cancellative monoids’, Manuscripta Math. 120 (2006), 253–264.Google Scholar
Chapman, S. T., Gotti, F. and Pelayo, R., ‘On delta sets and their realizable subsets in Krull monoids with cyclic class groups’, Colloq. Math. 137 (2014), 137–146.Google Scholar
Facchini, A., ‘Krull monoids and their application in module theory’, in: Algebras, Rings and their Representations (eds. Facchini, A., Fuller, K., Ringel, C. M. and Santa-Clara, C.) (World Scientific, Hackensack, NJ, 2006), 53–71.Google Scholar
Gao, W., Geroldinger, A. and Grynkiewicz, D. J., ‘Inverse zero-sum problems III’, Acta Arith. 141 (2010), 103–152.CrossRefGoogle Scholar
García-Sánchez, P. A., Ojeda, I. and Sánchez-R.-Navarro, A., ‘Factorization invariants in half-factorial affine semigroups’, Internat. J. Algebra Comput. 23 (2013), 111–122.Google Scholar
Geroldinger, A., ‘Additive group theory and non-unique factorizations’, in: Combinatorial Number Theory and Additive Group Theory, Advanced Courses in Mathematics CRM Barcelona (eds. Geroldinger, A. and Ruzsa, I.) (Birkhäuser, Basel, 2009), 1–86.CrossRefGoogle Scholar
Geroldinger, A., ‘Non-commutative Krull monoids: a divisor theoretic approach and their arithmetic’, Osaka J. Math. 50 (2013), 503–539.Google Scholar
Geroldinger, A. and Grynkiewicz, D. J., ‘On the structure of minimal zero-sum sequences with maximal cross number’, J. Comb. Number Theory 1(2) (2009), 9–26.Google Scholar
Geroldinger, A., Grynkiewicz, D. J. and Schmid, W. A., ‘The catenary degree of Krull monoids I’, J. Théor. Nombres Bordeaux 23 (2011), 137–169.Google Scholar
Geroldinger, A. and Halter-Koch, F., Non-Unique Factorizations. Algebraic, Combinatorial and Analytic Theory, Pure and Applied Mathematics, 278 (Chapman & Hall/CRC, Boca Raton, FL, 2006).Google Scholar
Geroldinger, A. and Yuan, P., ‘The set of distances in Krull monoids’, Bull. Lond. Math. Soc. 44 (2012), 1203–1208.CrossRefGoogle Scholar
Grynkiewicz, D. J., Structural Additive Theory, Developments in Mathematics (Springer, New York, 2013).Google Scholar
Halter-Koch, F., ‘Ideal systems’, in: An Introduction to Multiplicative Ideal Theory (Marcel Dekker, New York, 1998).Google Scholar
Kainrath, F., ‘Factorization in Krull monoids with infinite class group’, Colloq. Math. 80 (1999), 23–30.Google Scholar
Omidali, M., ‘The catenary and tame degree of numerical monoids generated by generalized arithmetic sequences’, Forum Math. 24 (2012), 627–640.Google Scholar
Philipp, A., A characterization of arithmetical invariants by the monoid of relations II: The monotone catenary degree and applications to semigroup rings, Semigroup Forum, to appear.Google Scholar
Reiher, C., ‘A proof of the theorem according to which every prime number possesses property B’, PhD Thesis, Rostock, 2010.Google Scholar
Savchev, S. and Chen, F., ‘Long minimal zero-sum sequences in the groups C 2 r−1 ⊕ C 2k ’, Integers 14 (2014), Paper A23.Google Scholar
Schmid, W. A., ‘Arithmetical characterization of class groups of the form ℤ∕nℤ ⊕ℤ ∕nℤ via the system of sets of lengths’, Abh. Math. Semin. Univ. Hambg. 79 (2009), 25–35.Google Scholar
Schmid, W. A., ‘Characterization of class groups of Krull monoids via their systems of sets of lengths: a status report’, in: Number Theory and Applications: Proceedings of the International Conferences on Number Theory and Cryptography (eds. Adhikari, S. D. and Ramakrishnan, B.) (Hindustan Book Agency, New Delhi, 2009), 189–212.Google Scholar
Schmid, W. A., ‘Inverse zero-sum problems II’, Acta Arith. 143 (2010), 333–343.Google Scholar
Schmid, W. A., ‘The inverse problem associated to the Davenport constant for C 2 ⊕ C 2 ⊕ C 2n , and applications to the arithmetical characterization of class groups’, Electron. J. Combin. 18(1) (2011), Research Paper 33.Google Scholar
Smertnig, D., ‘Sets of lengths in maximal orders in central simple algebras’, J. Algebra 390 (2013), 1–43.Google Scholar