Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T04:38:09.387Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CATENARY AND TAME DEGREES ON A NUMERICAL MONOID ARE EVENTUALLY PERIODIC

Part of: Semigroups

Published online by Cambridge University Press:  09 September 2014

SCOTT T. CHAPMAN ,
MARLY CORRALES ,
ANDREW MILLER ,
CHRIS MILLER  and
DHIR PATEL
SCOTT T. CHAPMAN*
Affiliation:
Sam Houston State University, Department of Mathematics, Box 2206, Huntsville, TX 77341, USA email [email protected]
MARLY CORRALES
Affiliation:
University of Southern California, Department of Mathematics, 3620 S. Vermont Ave., KAP 104, Los Angeles, CA 90089-2532, USA email [email protected]
ANDREW MILLER
Affiliation:
Amherst College, Department of Mathematics, Box 2239 P.O. 5000, Amherst, MA 01002-5000, USA email [email protected]
CHRIS MILLER
Affiliation:
The University of Wisconsin at Madison, Department of Mathematics, 480 Lincoln Dr., Madison, WI 53706-1325, USA email [email protected]
DHIR PATEL
Affiliation:
Rutgers University, Department of Mathematics, Hill Center for the Mathematical Sciences, 110 Frelinghuysen Rd., Piscataway, NJ 08854-8019, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 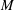$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M$ be a commutative cancellative monoid. For $m$ a nonunit in $M$, the catenary degree of 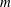$m$, denoted 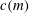$c(m)$, and the tame degree of 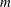$m$, denoted 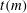$t(m)$, are combinatorial constants that describe the relationships between differing irreducible factorizations of 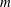$m$. These constants have been studied carefully in the literature for various kinds of monoids, including Krull monoids and numerical monoids. In this paper, we show for a given numerical monoid 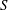$S$ that the sequences 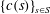$\{c(s)\}_{s\in S}$ and 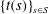$\{t(s)\}_{s\in S}$ are both eventually periodic. We show similar behavior for several functions related to the catenary degree which have recently appeared in the literature. These results nicely complement the known result that the sequence 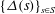$\{\Delta (s)\}_{s\in S}$ of delta sets of 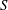$S$ also satisfies a similar periodicity condition.

Keywords

catenary degreetame degreenumerical monoid

MSC classification

Secondary: 20M13: Arithmetic theory of monoids 20M14: Commutative semigroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 289 - 300
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aguiló-Gost, F. and García-Sánchez, P. A., ‘Factorization and catenary degree in 3-generated numerical semigroups’, Electron. Notes Discrete Math. 34 (2009), 157–161.Google Scholar
Amos, J., Chapman, S. T., Hine, N. and Paixao, J., ‘Sets of lengths and unions of sets of lengths do not characterize numerical monoids’, Integers 7 (2007), #A50.Google Scholar
Baginski, P., Chapman, S. T., Rodriguez, R., Schaeffer, G. and She, Y., ‘On the delta set and catenary degree of Krull monoids with infinite cyclic divisor class group’, J. Pure Appl. Algebra 214 (2010), 1334–1339.Google Scholar
Blanco, V., García-Sánchez, P. A. and Geroldinger, A., ‘Semigroup-theoretical characterizations of arithmetical invariants with applications to numerical monoids and Krull monoids’, Illinois J. Math. 55 (2011), 1385–1414.CrossRefGoogle Scholar
Bowles, C., Chapman, S., Kaplan, N. and Resier, D., ‘Delta sets of numerical monoids’, J. Algebra Appl. 5 (2006), 1–24.Google Scholar
Chapman, S. T., García-Sánchez, P. A. and Llena, D., ‘The catenary and tame degree of numerical monoids’, Forum Math. 21 (2009), 117–129.Google Scholar
Chapman, S. T., García-Sánchez, P. A., Llena, D., Ponomarenko, V. and Rosales, J. C., ‘The catenary and tame degree in finitely generated commutative cancellative monoids’, Manuscripta Math. 120 (2006), 253–264.Google Scholar
Chapman, S. T., Holden, M. and Moore, T., ‘Full elasticity in atomic monoids and integral domains’, Rocky Mountain J. Math. 36 (2006), 1437–1455.Google Scholar
Chapman, S. T., Hoyer, R. and Kaplan, N., ‘Delta sets of numerical monoids are eventually periodic’, Aequationes Math. 77 (2009), 273–279.Google Scholar
Delgado, M., García-Sánchez, P. A. and Morais, J., ‘NumericalSgps, a GAP package for numerical semigroups’, current version number 0.97 (2011) available via http://www.gap-system.org/.Google Scholar
Foroutan, A., ‘Monotone chains of factorizations’, in: Focus on Commutative Rings Research (ed. Badawi, A.) (Nova Science, New York, 2006), 107–130.Google Scholar
Foroutan, A. and Geroldinger, A., Monotone Chains of Factorizations in C-Monoids, Lecture Notes in Pure and Applied Mathematics, 241 (Marcel Dekker, New York, 2005), 99–113.Google Scholar
Geroldinger, A., The catenary degree and tameness of factorizations in weakly Krull domains, Lecture Notes in Pure and Applied Mathematics, 189 (Marcel Dekker, New York, 1997), 113–154.Google Scholar
Geroldinger, A., Grynkiewicz, D. J. and Schmid, W. A., ‘The catenary degree of Krull monoids I’, J. Théor. Nombres Bordeaux 23 (2011), 137–169.Google Scholar
Geroldinger, A. and Halter-Koch, F., Non-Unique Factorizations: Algebraic, Combinatorial, and Analytic Theory (Chapman and Hall/CRC, Boca Raton, FL, 2006).Google Scholar
Geroldinger, A. and Yuan, P., ‘The monotone catenary degree of Krull monoids’, Results Math. 63 (2013), 999–1031.CrossRefGoogle Scholar
Halter-Koch, F., ‘The tame degree and related invariants of non-unique factorizations’, Acta Math. Univ. Ostrav. 16 (2008), 57–68.Google Scholar
Omidali, M., ‘The catenary and tame degree of numerical monoids generated by generalized arithmetic sequences’, Forum Math. 24 (2012), 627–640.Google Scholar
Philipp, A., ‘A characterization of arithmetical invariants by the monoid of relations II: The monotone catenary degree and applications to semigroup rings’, Semigroup Forum 81 (2010), 424–434.Google Scholar
Rosales, J. C. and García-Sánchez, P. A., Finitely Generated Commutative Monoids (Nova Science, New York, 1999).Google Scholar
Rosales, J. C. and García-Sánchez, P. A., Numerical Semigroups, Vol. 20 (Springer, New York, 2009).Google Scholar