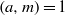Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Banks, William
Finch, Carrie
Luca, Florian
Pomerance, Carl
and
Stănică, Pantelimon
2014.
Sierpiński and Carmichael numbers.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 1,
p.
355.
Wright, Thomas
2015.
Variants of Korselt’s Criterion.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 4,
p.
869.
Banks, William D.
and
Freiberg, Tristan
2016.
Carmichael numbers and the sieve.
Journal of Number Theory,
Vol. 165,
Issue. ,
p.
15.
Banks, William
2021.
Arithmetic progressions of Carmichael numbers in a reduced residue class.
Journal of Number Theory,
Vol. 228,
Issue. ,
p.
22.