BOUNDEDNESS OF MAXIMAL FUNCTIONS ON NONDOUBLING PARABOLIC MANIFOLDS WITH ENDS

Abstract

Let 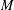$M$ be a nondoubling parabolic manifold with ends. First, this paper investigates the boundedness of the maximal function associated with the heat semigroup 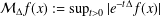${\mathcal{M}}_{\unicode[STIX]{x1D6E5}}f(x):=\sup _{t>0}|e^{-t\unicode[STIX]{x1D6E5}}f(x)|$ where 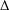$\unicode[STIX]{x1D6E5}$ is the Laplace–Beltrami operator acting on 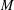$M$. Then, by combining the subordination formula with the previous result, we obtain the weak type 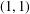$(1,1)$ and 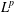$L^{p}$ boundedness of the maximal function 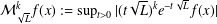${\mathcal{M}}_{\sqrt{L}}^{k}f(x):=\sup _{t>0}|(t\sqrt{L})^{k}e^{-t\sqrt{L}}f(x)|$ on 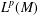$L^{p}(M)$ for 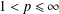$1<p\leq \infty$ where 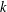$k$ is a nonnegative integer and $L$ is a nonnegative self-adjoint operator satisfying a suitable heat kernel upper bound. An interesting thing about the results is the lack of both doubling condition of 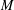$M$ and the smoothness of the operators’ kernels.