Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-19T14:05:03.183Z Has data issue: false hasContentIssue false
  • English
  • Français

BOUNDARY BLOW-UP SOLUTIONS TO EQUATIONS INVOLVING THE INFINITY LAPLACIAN

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  23 August 2022

CUICUI LI ,
FANG LIU  and
PEIBIAO ZHAO
CUICUI LI
Affiliation:
Department of Mathematics, School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, PR China e-mail: [email protected]
FANG LIU*
Affiliation:
Department of Mathematics, School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, PR China
PEIBIAO ZHAO
Affiliation:
Department of Mathematics, School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, PR China e-mail: [email protected]
*
e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the boundary blow-up problem related to the infinity Laplacian

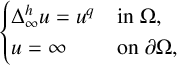$$ \begin{align*}\begin{cases} \Delta_{\infty}^h u=u^q &\mathrm{in}\; \Omega, \\ u=\infty &\mathrm{on} \;\partial\Omega, \end{cases} \end{align*} $$

where 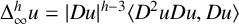$\Delta _{\infty }^h u=|Du|^{h-3} \langle D^2uDu,Du \rangle $ is the highly degenerate and h-homogeneous operator associated with the infinity Laplacian arising from the stochastic game named Tug-of-War. When 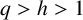$q>h>1$ , we establish the existence of the boundary blow-up viscosity solution. Moreover, when the domain satisfies some regular condition, we establish the asymptotic estimate of the blow-up solution near the boundary. As an application of the asymptotic estimate and the comparison principle, we obtain the uniqueness result of the large solution. We also give the nonexistence of the large solution for the case 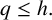$q \leq h.$

Keywords

infinity Laplacianboundary blow-up solutioncomparison principleboundary asymptotic estimate

MSC classification

Primary: 35J60: Nonlinear elliptic equations 35J70: Degenerate elliptic equations 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 114 , Issue 3 , June 2023 , pp. 337 - 358
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Florica Cirstea

This work was supported by National Natural Science Foundation of China (Nos. 11501292, 11871275 and 12141104).

References

Abderrahim, E., Xavier, D., Zakaria, L. and Olivier, L., ‘Nonlocal infinity Laplacian equation on graphs with applications in image processing and machine learning’, Math. Comput. Simulation 102 (2014), 153–163.CrossRefGoogle Scholar
Aronsson, G., ‘Extension of functions satisfying Lipschitz conditions’, Ark. Mat. 6 (1967), 551–561.CrossRefGoogle Scholar
Aronsson, G., Crandall, M. G. and Juutinen, P., ‘A tour of the theory of absolutely minimizing functions’, Bull. Amer. Math. Soc. (N.S.) 41 (2004), 439–505.CrossRefGoogle Scholar
Bhattacharya, T. and Mohammed, A., ‘On solutions to Dirichlet problems involving the infinity-Laplacian’, Adv. Calc. Var. 4 (2011), 445–487.CrossRefGoogle Scholar
Bhattacharya, T. and Mohammed, A., ‘Inhomogeneous Dirichlet problems involving the infinity-Laplacian’, Adv. Differential Equations 17(3–4) (2012), 225–266.CrossRefGoogle Scholar
Caselles, V., Morel, J. M. and Sbert, C., ‘An axiomatic approach to image interpolation’, IEEE Trans. Image Process 7 (1998), 376–386.CrossRefGoogle ScholarPubMed
Cîrstea, F. and Rǎdulescu, V., ‘ Uniqueness of the blow-up boundary solution of logistic equations with absorption ’, C. R. Math. Acad. Sci. Paris, Sér. I 335 (2002), 447–452.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V., ‘ Asymptotics for the blow-up boundary solution of the logistic equation with absorption ’, C. R. Math. Acad. Sci. Paris, Sér. I 336 (2003), 231–236.CrossRefGoogle Scholar
Cîrstea, F. and Rǎdulescu, V., ‘Nonlinear problems with boundary blow-up: a Karamata regular variation theory approach’, Asymptot. Anal. 46 (2006), 275–298.Google Scholar
Crandall, M. G., ‘A visit with the $\infty$ -Laplacian’, in: Calculus of Variations and Non-linear Partial Differential Equations (CIME, Cetraro Italy, 2005), Lecture Notes in Mathematics, 1927 (Springer, Berlin, 2008), 75–122.CrossRefGoogle Scholar
Crandall, M. G., Evans, L. C. and Gariepy, R. F., ‘Optimal Lipschitz extensions and the infinity Laplacian,’ Calc. Var. Partial Differential Equations 13 (2001), 123–139.CrossRefGoogle Scholar
Crandall, M. G., Ishii, H. and Lions, P. L., ‘User’s guide to viscosity solutions of second order partial differential equations’, Bull. Amer. Math. Soc. (N. S.) 27 (1992), 1–67.CrossRefGoogle Scholar
Elmoataz, A., Toutain, M. and Tenbrinck, D., ‘On the $p$ -Laplacian and $\infty$ -Laplacian on graphs with applications in image and data processing’, SIAM J. Imaging Sci. 8(4) (2015), 2412–2451.CrossRefGoogle Scholar
Evans, L. C. and Gangbo, W., ‘Differential equations methods for the Monge–Kantorovich mass transfer problem’, Mem. Amer. Math. Soc. 137(653) (1999), viii+66 pages.Google Scholar
Fraile, J. M., Medina, P., López-Gómez, J. and Merino, S., ‘Elliptic eigenvalue problems and unbounded continua of positive solutions of a semilinear equation’, J. Differential Equations 127 (1996), 295–319.CrossRefGoogle Scholar
García-Melián, J., Gómez-Reñasco, R., López-Gómez, J. and Sabinade, J., ‘Pointwise growth and uniqueness of positive solutions for a class of sublinear elliptic problems where bifurcation from infinity occurs,’ Arch. Ration. Mech. Anal. 145 (1998), 261–289.Google Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order. Reprint of the 1998 edition, Classics in Mathematics, 224 (Springer-Verlag, Berlin, 2001).CrossRefGoogle Scholar
Juutinen, P., ‘The boundary Harnack inequality for infinity harmonic functions in Lipschitz domains satisfying the interior ball condition’, Nonlinear Anal. 69(7) (2008), 1941–1944.CrossRefGoogle Scholar
Juutinen, P. and Rossi, J. D., ‘Large solutions for the infinity Laplacian’, Adv. Calc. Var. 1(3) (2008), 271–289.CrossRefGoogle Scholar
Lasry, J. M. and Lions, P. L., ‘Nonlinear elliptic equations with singular boundary conditions and stochastic control with state constraints. I. The model problem’, Math. Ann. 283 (1989), 583–630.CrossRefGoogle Scholar
Liu, F., ‘An inhomogeneous evolution equation involving the normalized infinity Laplacian with a transport term’, Commun. Pure Appl. Anal. 17(6) (2018), 2395–2421.CrossRefGoogle Scholar
Liu, F. and Yang, X., ‘Solutions to an inhomogeneous equation involving infinity-Laplacian’, Nonlinear Anal. 75 (2012), 5693–5701.CrossRefGoogle Scholar
Liu, Q. and Schikorra, A., ‘ General existence of solutions to dynamic programming equations ’, Commun. Pure Appl. Anal. 14 (2015), 167–184.CrossRefGoogle Scholar
López-Soriano, R., Navarro-Climent, J. C. and Rossi, J. D., ‘The infinity Laplacian with a transport term’, J. Math. Anal. Appl. 398 (2013), 752–765.CrossRefGoogle Scholar
Lu, G. and Wang, P., ‘A uniqueness theorem for degenerate elliptic equations’, Semin. Interdiscip. Mat. 7 (2008), 207–222.Google Scholar
Lu, G. and Wang, P., ‘Inhomogeneous infinity Laplace equation’, Adv. Math. 217(4) (2008), 1838–1868.CrossRefGoogle Scholar
Lu, G. and Wang, P., ‘A PDE perspective of the normalized infinity Laplacian,’ Comm. Partial Differential Equations 33(10) (2008), 1788–1817.CrossRefGoogle Scholar
Mi, L., ‘Blow-up rates of large solutions for infinity Laplace equations’, Appl. Math. Comput. 298 (2017), 36–44.Google Scholar
Mohammed, A. and Mohammed, S., ‘On boundary blow-up solutions to equations involving the $\infty$ -Laplacian’, Nonlinear Anal. 74 (2011), 5238–5252.CrossRefGoogle Scholar
Mohammed, A. and Mohammed, S., ‘Boundary blow-up solutions to degenerate elliptic equations with non-monotone inhomogeneous terms’, Nonlinear Anal. 75 (2012), 3249–3261.CrossRefGoogle Scholar
Ouyang, T., ‘On the positive solutions of semilinear equation $\varDelta u+\lambda u-h{u}^p = 0$ on the compact manifolds’, Trans. Amer. Math. Soc. 331 (1992), 503–527.Google Scholar
Peres, Y., Pete, G. and Somersille, S., ‘Biased tug-of-war, the biased infinity Laplacian, and comparison with exponential cones’, Calc. Var. Partial Differential Equations 38(3–4) (2010), 541–564.CrossRefGoogle Scholar
Peres, Y., Schramm, O., Sheffield, S. and Wilson, D., ‘Tug-of-war and the infinity Laplacian’, J. Amer. Math. Soc. 22(1) (2009), 167–210.CrossRefGoogle Scholar
Portilheiro, M. and Vázquez, J. L., ‘Degenerate homogeneous parabolic equations associated with the infinity-Laplacian’, Calc. Var. Partial Differential Equations 46(3–4) (2013), 705–724.CrossRefGoogle Scholar
Rossi, J. D., ‘Tug-of-war games and PDEs’, Proc. Roy. Soc. Edinburgh Sect. A 141 ( 2 ) (2011), 319–369.CrossRefGoogle Scholar
Wang, W., Gong, H. and Zheng, S., ‘Asymptotic estimates of boundary blow-up solutions to the infinity Laplace equations’, J. Differential Equations 256 (2014), 3721–3742.CrossRefGoogle Scholar
Zhang, Z., ‘Boundary behavior of large viscosity solutions to infinity Laplace equations’, Z. Angew. Math. Phys. 66 (2015), 1453–1472.CrossRefGoogle Scholar