Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-08T18:34:11.769Z Has data issue: false hasContentIssue false
  • English
  • Français

A BOUND FOR SIMILARITY CONDITION NUMBERS OF UNBOUNDED OPERATORS WITH HILBERT–SCHMIDT HERMITIAN COMPONENTS

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  12 September 2014

MICHAEL GIL’
MICHAEL GIL’*
Affiliation:
Department of Mathematics, Ben Gurion University of the Negev, P.O. Box 653, Beer-Sheva 84105, Israel email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 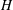$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ be a linear unbounded operator in a Hilbert space. It is assumed that the resolvent of 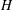$H$ is a compact operator and 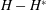$H-H^*$ is a Hilbert–Schmidt operator. Various integro-differential operators satisfy these conditions. It is shown that 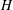$H$ is similar to a normal operator and a sharp bound for the condition number is suggested. We also discuss applications of that bound to spectrum perturbations and operator functions.

Keywords

operatorssimilaritycondition numbersspectrum perturbationsnorm of operator function

MSC classification

Secondary: 47A30: Norms (inequalities, more than one norm, etc.) 47A55: Perturbation theory 47A56: Functions whose values are linear operators (operator and matrix valued functions, etc., including analytic and meromorphic ones) 47B10: Operators belonging to operator ideals (nuclear, $p$-summing, in the Schatten-von Neumann classes, etc.) 47B40: Spectral operators, decomposable operators, well-bounded operators, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 331 - 342
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Benamara, N. E. and Nikolskii, N. K., ‘Resolvent tests for similarity to a normal operator’, Proc. Lond. Math. Soc. (3) 78 (1999), 585–626.Google Scholar
Betcke, T., Chandler-Wilde, S. N., Graham, I. G., Langdon, S. and Lindner, M., ‘Condition number estimates for combined potential integral operators in acoustics and their boundary element discretisation’, Numer. Methods Partial Differential Equations 27 (2011), 31–69.Google Scholar
Bhatia, R. and Rosenthal, P., ‘How and why to solve the operator equation A X − X B = Y’, Bull. Lond. Math. Soc. 29 (1997), 1–21.Google Scholar
van Casteren, J. A., ‘Operators similar to unitary or selfadjoint ones’, Pacific J. Math. 104(1) (1983), 241–255.Google Scholar
Chandler-Wilde, S. N., Graham, I. G., Langdon, S. and Lindner, M., ‘Condition number estimates for combined potential boundary integral operators in acoustic scattering’, J. Integral Equations Appl. 21 (2009), 229–279.Google Scholar
Chen, G., Wei, Y. and Xue, Y., ‘The generalized condition numbers of bounded linear operators in Banach spaces’, J. Aust. Math. Soc. 76 (2004), 281–290.Google Scholar
Daleckii, Yu. L. and Krein, M. G., Stability of Solutions of Differential Equations in Banach Space (American Mathematical Society, Providence, RI, 1971).Google Scholar
Faddeev, M. M. and Shterenberg, R. G., ‘On similarity of differential operators to a selfadjoint one’, Math. Notes 72 (2002), 292–303.CrossRefGoogle Scholar
Gil’, M. I., Operator Functions and Localization of Spectra, Lecture Notes in Mathematics, 1830 (Springer, Berlin, 2003).Google Scholar
Gil’, M. I., ‘Perturbations of functions of diagonalizable matrices’, Electron. J. Linear Algebra 20 (2010), 303–313.Google Scholar
Gil’, M. I., ‘Matrix equations with diagonalizable coefficients’, Gulf J. Math. 1 (2013), 98–104.Google Scholar
Gil’, M. I., ‘A bound for condition numbers of matrices’, Electron. J. Linear Algebra 27 (2014), 162–171.Google Scholar
Gohberg, I. C. and Krein, M. G., Introduction to the Theory of Linear Nonselfadjoint Operators, Translations of Mathematical Monographs, 18 (American Mathematical Society, Providence, RI, 1969).Google Scholar
Karabash, I. M., ‘J-selfadjoint ordinary differential operators similar to selfadjoint operators’, Methods Funct. Anal. Topology 6(2) (2000), 22–49.Google Scholar
Karabash, I. M., Kostenko, A. S. and Malamud, M. M., ‘The similarity problem for J-nonnegative Sturm–Liouville operators’, J. Differential Equations 246 (2009), 964–997.Google Scholar
Kostenko, A., ‘The similarity problem for indefinite Sturm–Liouville operators with periodic coefficients’, Oper. Matrices 5(4) (2011), 707–722.Google Scholar
Kostenko, A., ‘The similarity problem for indefinite Sturm–Liouville operators and the HELP inequality’, Adv. Math. 246 (2013), 368–413.Google Scholar
Malamud, M. M., ‘Similarity of a triangular operator to a diagonal operator’, J. Math. Sci. 115(2) (2003), 2199–2222.Google Scholar
Markus, A., Introduction to the Spectral Theory of Polynomial Operator Pencils, Translations of Mathematical Monographs, 71 (American Mathematical Society, Providence, RI, 1988).Google Scholar
Parter, S. V. and Wong, S.-P., ‘Preconditioning second-order elliptic operators: condition numbers and the distribution of the singular values’, J. Sci. Comput. 6(2) (1991), 129–157.Google Scholar
Pruvost, B., ‘Analytic equivalence and similarity of operators’, Integral Equations Operator Theory 44 (2002), 480–493.Google Scholar
Rosenblum, M., ‘On the operator equation B X − X A = Q’, Duke Math. J. 23 (1956), 263–270.Google Scholar
Seidel, M. and Silbermann, B., ‘Finite sections of band-dominated operators, norms, condition numbers and pseudospectra’, in: Operator Theory: Advances and Applications,Vol. 228 (Springer, Basel, 2013), 375–390.Google Scholar