Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Paul, Kallol
Sain, Debmalya
and
Mal, Arpita
2018.
Approximate Birkhoff–James orthogonality in the space of bounded linear operators.
Linear Algebra and its Applications,
Vol. 537,
Issue. ,
p.
348.
Mal, Arpita
Paul, Kallol
Rao, T. S. S. R. K.
and
Sain, Debmalya
2019.
Approximate Birkhoff–James orthogonality and smoothness in the space of bounded linear operators.
Monatshefte für Mathematik,
Vol. 190,
Issue. 3,
p.
549.
Wójcik, Paweł
2019.
Extensions of linear operators from hyperplanes and strong uniqueness of best approximation in L(X,W).
Journal of Approximation Theory,
Vol. 246,
Issue. ,
p.
28.
Sain, Debmalya
Mal, Arpita
and
Paul, Kallol
2020.
Some remarks on Birkhoff–James orthogonality of linear operators.
Expositiones Mathematicae,
Vol. 38,
Issue. 1,
p.
138.
Mal, Arpita
and
Paul, Kallol
2020.
Characterization of k-smooth operators between Banach spaces.
Linear Algebra and its Applications,
Vol. 586,
Issue. ,
p.
296.
Sain, Debmalya
2021.
Orthogonality and smoothness induced by the norm derivatives.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 3,
Singla, Sushil
2021.
Gateaux derivative of C⁎ norm.
Linear Algebra and its Applications,
Vol. 629,
Issue. ,
p.
208.
Mal, Arpita
Dey, Subhrajit
and
Paul, Kallol
2022.
Characterization of k-smoothness of operators defined between infinite-dimensional spaces.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 18,
p.
3477.
Wójcik, Paweł
2022.
Vertices of the unit ball of subspaces in L(H) and strong unicity of best approximation in L(l22).
Linear Algebra and its Applications,
Vol. 632,
Issue. ,
p.
281.
Mal, Arpita
Paul, Kallol
and
Dey, Subhrajit
2022.
Characterization of extreme contractions through k-smoothness of operators.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 20,
p.
5301.
Grover, Priyanka
and
Singla, Sushil
2023.
Subdifferential set of the joint numerical radius of a tuple of matrices.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 17,
p.
2709.
Wójcik, Paweł
and
Zamani, Ali
2023.
From norm derivatives to orthogonalities in Hilbert C*-modules.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 6,
p.
875.
Conde, C.
and
Feki, K.
2024.
On approximate A-seminorm and A-numerical radius orthogonality of operators.
Acta Mathematica Hungarica,
Vol. 173,
Issue. 1,
p.
227.
Sain, Debmalya
Sohel, Shamim
and
Paul, Kallol
2024.
On k-smoothness of operators between Banach spaces.
Bulletin des Sciences Mathématiques,
Vol. 196,
Issue. ,
p.
103486.
Mal, Arpita
Paul, Kallol
and
Sain, Debmalya
2024.
Birkhoff–James Orthogonality and Geometry of Operator Spaces.
p.
47.
Chmieliński, Jacek
Ghosh, Souvik
Paul, Kallol
and
Sain, Debmalya
2025.
Smoothness and approximate smoothness in normed linear spaces and operator spaces.
Annals of Functional Analysis,
Vol. 16,
Issue. 2,
Ghosh, Souvik
Paul, Kallol
and
Sain, Debmalya
2025.
Orthogonality induced by norm derivatives: a new geometric constant and symmetry.
Aequationes mathematicae,
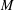 $M$-IDEALS
$M$-IDEALS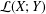 ${\mathcal{L}}(X;Y)$ under the assumption that
${\mathcal{L}}(X;Y)$ under the assumption that 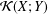 ${\mathcal{K}}(X;Y)$ is an
${\mathcal{K}}(X;Y)$ is an 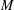 $M$-ideal in
$M$-ideal in 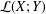 ${\mathcal{L}}(X;Y)$. Moreover, we survey the known results, as well as giving some new and more general ones. Furthermore, we characterize an approximate Birkhoff orthogonality in
${\mathcal{L}}(X;Y)$. Moreover, we survey the known results, as well as giving some new and more general ones. Furthermore, we characterize an approximate Birkhoff orthogonality in 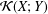 ${\mathcal{K}}(X;Y)$.
${\mathcal{K}}(X;Y)$.

