Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T07:41:00.879Z Has data issue: false hasContentIssue false
  • English
  • Français

BASES OF 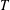$T$-EQUIVARIANT COHOMOLOGY OF BOTT–SAMELSON VARIETIES

Part of: Homology and cohomology theories

Published online by Cambridge University Press:  05 May 2017

VLADIMIR SHCHIGOLEV
VLADIMIR SHCHIGOLEV*
Affiliation:
Financial University under the Government of the Russian Federation, 49 Leningradsky Prospekt, Moscow, Russia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct combinatorial bases of the 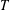$T$-equivariant cohomology 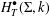$H_{T}^{\bullet }(\unicode[STIX]{x1D6F4},k)$ of the Bott–Samelson variety 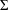$\unicode[STIX]{x1D6F4}$ under some mild restrictions on the field of coefficients 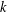$k$. These bases allow us to prove the surjectivity of the restrictions 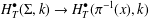$H_{T}^{\bullet }(\unicode[STIX]{x1D6F4},k)\rightarrow H_{T}^{\bullet }(\unicode[STIX]{x1D70B}^{-1}(x),k)$ and 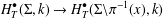$H_{T}^{\bullet }(\unicode[STIX]{x1D6F4},k)\rightarrow H_{T}^{\bullet }(\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D70B}^{-1}(x),k)$, where 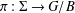$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6F4}\rightarrow G/B$ is the canonical resolution. In fact, we also construct bases of the targets of these restrictions by picking up certain subsets of certain bases of 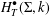$H_{T}^{\bullet }(\unicode[STIX]{x1D6F4},k)$ and restricting them to 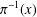$\unicode[STIX]{x1D70B}^{-1}(x)$ or $\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D70B}^{-1}(x)$ respectively. As an application, we calculate the cohomology of the costalk-to-stalk embedding for the direct image 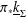$\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{k}_{_{\unicode[STIX]{x1D6F4}}}$. This algorithm avoids division by 2, which allows us to re-establish 2-torsion for parity sheaves in Braden’s example, Braden and Williamson [‘Modular intersection cohomology complexes on flag varieties’, Math. Z.272(3–4) (2012), 697–727].

Keywords

Bott–Samelson varietyequivariant cohomologyparity sheaves

MSC classification

Primary: 55N91: Equivariant homology and cohomology
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 1 , February 2018 , pp. 80 - 126
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Arabia, A., ‘Cohomologie T-équivariante de la variété de drapeaux d’un groupe de Kač–Moody’, Bull. Soc. Math. France 117 (1989), 129–165.Google Scholar
Arabia, A., ‘Classes d’Euler équivariantes et points rationnellement lisses’, Ann. Inst. Fourier (Grenoble) 48(3) (1998), 861–912.CrossRefGoogle Scholar
Atiyah, M. F. and Bott, R., ‘The moment map and equivariant cohomology’, Topology 23(1) (1984), 1–28.Google Scholar
Bernstein, J. and Lunts, V., Equivariant Sheaves and Functors, Lecture Notes in Mathematics, 1578 (Springer, Berlin, 1994).CrossRefGoogle Scholar
Braden, T. and Williamson, G., ‘Modular intersection cohomology complexes on flag varieties’, Math. Z. 272(3–4) (2012), 697–727.Google Scholar
Brion, M., ‘Equivariant cohomology and equivariant intersection theory’, in: Representation Theories and Algebraic Geometry (Montreal, PQ, 1997) (Kluwer Academic Publishers, Dordrecht, 1998), 1–37.Google Scholar
Dimca, A., Sheaves in Topology (Universitext, Springer, Berlin, 2004).Google Scholar
Fiebig, P., ‘An upper bound on exceptional characteristics for Lusztig’s character formula’, J. reine angew. Math. 673 (2012), 1–31.Google Scholar
Fiebig, P. and Williamson, G., ‘Parity sheaves, moment graphs and the p-smooth locus of Schubert varieties’, Ann. Inst. Fourier (Grenoble) 64(2) (2014), 489–536.CrossRefGoogle Scholar
Gaussent, S., ‘Corrections and new results on the fibre of the Bott–Samelson resolution’, Indag. Math. (N.S.) 14(1) (2003), 31–33.Google Scholar
Härterich, M., ‘The T-equivariant cohomology of Bott–Samelson varieties’, Preprint, 2004, arXiv:math/0412337v1.Google Scholar
Iversen, B., Cohomology of Sheves (Universitext, Springer, Berlin–Heidelberg–New York, 1986).Google Scholar
Jantzen, J. C., ‘Moment graphs and representations’, in: Inst. Fourier, Geometric Methods in Representation Theory, Summer School Proceedings (Birkhäuser, Basel, 2008).Google Scholar
Kumar, S., Kac–Moody Groups, Their Flag Varieties and Representation Theory, Progress in Mathematics, 204 (Springer, Boston, 2002).Google Scholar
Mautner, C., Juteau, D. and Williamson, G., ‘Parity sheaves’, J. Amer. Math. Soc. 27(4) (2014), 1169–1212.Google Scholar
Quillen, D., ‘The spectrum of an equivariant cohomology ring: I’, Ann. of Math. (2) 94(3) (1971), 549–572.Google Scholar
Shchigolev, V., ‘On decomposition of Bott–Samelson sheaves’, J. Algebra 406 (2014), 376–418.Google Scholar