Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T08:39:46.057Z Has data issue: false hasContentIssue false
  • English
  • Français

Balanced directed cycle designs based on cyclic groups

Part of: Designs and configurations Permutation groups

Published online by Cambridge University Press:  09 April 2009

Chaufah Nilrat  and
Cheryl E. Praeger
Chaufah Nilrat
Affiliation:
Faculty of Science, Department of Mathematics, Prince of Songkla University, Haad Yai, Thailand
Cheryl E. Praeger
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands WA 6907, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A balanced directed cycle design with parameters (υ, k, 1), sometimes called a (υ, k, 1)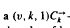-design, is a decomposition of the complete directed graph 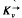into edge disjoint directed cycles of length k. A complete classification is given of (υ, k, 1)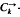-designs admitting the holomorph {øa, b: x ↦ ax + b∣ a, b ∈ Zυ, (a, υ1) = 1} of the cyclic group Zυ as a group of automorphisms. In particular it is shown that such a design exists if and ony if one of (a) k = 2, (b) p ≡ 1 (mod k) for each prime p dividing υ, or (c) k is the least prime dividing υ, k2 does not divide υ, and p ≡ 1 (mod k) for each prime p < k dividing υ.

MSC classification

Secondary: 05B30: Other designs, configurations 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 58 , Issue 2 , April 1995 , pp. 210 - 218
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Bermond, J. C. and Sotteau, D., ‘Graph decompositions and G-designs’, Proceedings of the Fifth British Combinatorial Conference, Cong. Numer. 15 (1975), 53–72.Google Scholar
[2]Brand, N. and Huffman, W. C., ‘Mendelsohn designs admitting the affine group’, Geom. Dedicata 22 (1987), 173–196.CrossRefGoogle Scholar
[3]Hell, P. and Rosa, A., ‘Graph decompositions, handcuffed prisoners and balanced P-designs’, Discrete Math. 2 (1972), 229–252.CrossRefGoogle Scholar
[4]Praeger, C. E., ‘Balanced directed cycle designs based on groups’, Discrete Math. 92 (1991), 275–290.CrossRefGoogle Scholar