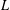Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T16:03:35.815Z Has data issue: false hasContentIssue false
  • English
  • Français

AVERAGES OF TWISTED $L$-FUNCTIONS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 June 2015

JULIA JACKSON  and
ANDREW KNIGHTLY
JULIA JACKSON
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, OK 73019-3103, USA email [email protected]
ANDREW KNIGHTLY*
Affiliation:
Department of Mathematics and Statistics, University of Maine, Orono, ME 04469-5752, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use a relative trace formula on 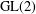$\text{GL}(2)$ to compute a sum of twisted modular 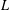$L$-functions anywhere in the critical strip, weighted by a Fourier coefficient and a Hecke eigenvalue. When the weight 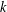$k$ or level 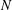$N$ is sufficiently large, the sum is nonzero. Specializing to the central point, we show in some cases that the resulting bound for the average is as good as that predicted by the Lindelöf hypothesis in the 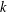$k$ and 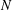$N$ aspects.

Keywords

relative trace formulaL-functionsmodular forms

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 2 , October 2015 , pp. 207 - 236
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abramowitz, N. and Stegun, I. (eds), Handbook of Mathematical Functions (Dover, New York, 1965).Google Scholar
Akbary, A., ‘Non-vanishing of weight k modular L-functions with large level’, J. Ramanujan Math. Soc. 14(1) (1999), 37–54.Google Scholar
Bennett, M., Ellenberg, J. and Ng, N., ‘The Diophantine equation A 4 + 2𝛿B 2 = C n’, Int. J. Number Theory 6(2) (2010), 311–338.CrossRefGoogle Scholar
Bump, D., Automorphic Forms and Representations, Cambridge Studies in Advanced Mathematics, 55 (Cambridge University Press, Cambridge, 1998).Google Scholar
Duke, W., ‘The critical order of vanishing of automorphic L-functions with large level’, Invent. Math. 119(1) (1995), 165–174.CrossRefGoogle Scholar
Ellenberg, J., ‘Galois representations attached to Q -curves and the generalized Fermat equation A 4 + B 2 = C p’, Amer. J. Math. 126(4) (2004), 763–787.CrossRefGoogle Scholar
Ellenberg, J., ‘On the error term in Duke’s estimate for the average special value of L-functions’, Canad. Math. Bull. 48(4) (2005), 535–546.CrossRefGoogle Scholar
Feigon, B. and Whitehouse, D., ‘Averages of central L-values of Hilbert modular forms with an application to subconvexity’, Duke Math. J. 149(2) (2009), 347–410.CrossRefGoogle Scholar
Fomenko, O., ‘Application of the Petersson formula for a bilinear form in Fourier coefficients of parabolic forms’, J. Math. Sci. 79(5) (1996), 1359–1372; translated from the Russian.CrossRefGoogle Scholar
Guo, J., ‘On the positivity of the central critical values of automorphic L-functions for GL(2)’, Duke Math. J. 83(1) (1996), 157–190.CrossRefGoogle Scholar
Holowinsky, R. and Templier, N., ‘First moment of Rankin–Selberg central L-values and subconvexity in the level aspect’, Ramanujan J. 33(1) (2014), 131–155.CrossRefGoogle Scholar
Iwaniec, H., Luo, W. and Sarnak, P., ‘Low lying zeros of families of L-functions’, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.CrossRefGoogle Scholar
Iwaniec, H. and Michel, P., ‘The second moment of the symmetric square L-functions’, Ann. Acad. Sci. Fenn. Math. 26(2) (2001), 465–482.Google Scholar
Iwaniec, H. and Sarnak, P., ‘The non-vanishing of central values of automorphic L-functions and Landau–Siegel zeros’, Israel J. Math. 120 (2000), 155–177.CrossRefGoogle Scholar
Iwaniec, H. and Sarnak, P., ‘Perspectives on the analytic theory of L-functions’, Geom. Funct. Anal. Special volume (Part II) (2000), 705–741.Google Scholar
Kamiya, Y., ‘Certain mean values and non-vanishing of automorphic L-functions with large level’, Acta Arith. 93(2) (2000), 157–176.CrossRefGoogle Scholar
Knightly, A. and Li, C., Traces of Hecke Operators, Mathematical Surveys and Monographs, 133 (Providence, RI, American Mathematical Society, 2006).CrossRefGoogle Scholar
Knightly, A. and Li, C., ‘Weighted averages of modular L-values’, Trans. Amer. Math. Soc. 362(3) (2010), 1423–1443.CrossRefGoogle Scholar
Knightly, A. and Li, C., ‘Kuznetsov’s formula and the Hecke eigenvalues of Maass forms’, Mem. Amer. Math. Soc. 224(1055) (2013).Google Scholar
Kohnen, W. and Sengupta, J., ‘On quadratic character twists of Hecke L-functions attached to cusp forms of varying weights at the central point’, Acta Arith. 99(1) (2001), 61–66.CrossRefGoogle Scholar
Li, S.-C. and Masri, R., ‘Nonvanishing of Rankin–Selberg L-functions for Hilbert modular forms’, Ramanujan J. 34(2) (2014), 227–236.CrossRefGoogle Scholar
Michel, P. and Ramakrishnan, D., Consequences of the Gross–Zagier Formulae: Stability of Average L-Values, Subconvexity, and Non-Vanishing mod p, Number Theory, Analysis and Geometry, 437–459 (Springer, New York, 2012).Google Scholar
Nelson, P., ‘Stable averages of central values of Rankin–Selberg L-functions: some new variants’, J. Number Theory 133(8) (2013), 2588–2615.CrossRefGoogle Scholar
Ramakrishnan, D. and Rogawski, J., ‘Average values of modular L-series via the relative trace formula’, Pure Appl. Math. Q. 1(4) (2005), 701–735.CrossRefGoogle Scholar
Sengupta, J., ‘The central critical value of automorphic L-functions’, C. R. Math. Rep. Acad. Sci. Can. 22(2) (2000), 82–85.Google Scholar
Serre, J.-P., ‘RĂ©partition asymptotique des valeurs propres de l’opĂ©rateur de Hecke T p’, J. Amer. Math. Soc. 10(1) (1997), 75–102.CrossRefGoogle Scholar