Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dooley, A. H.
and
Mortiss, G.
2006.
On the Critical Dimension and AC Entropy for Markov Odometers.
Monatshefte für Mathematik,
Vol. 149,
Issue. 3,
p.
193.
Dooley, Anthony H.
and
Mortiss, Genevieve
2007.
The critical dimensions of Hamachi shifts.
Tohoku Mathematical Journal,
Vol. 59,
Issue. 1,
Danilenko, Alexandre I.
and
Rudolph, Daniel J.
2009.
Conditional entropy theory in infinite measure and a question of Krengel.
Israel Journal of Mathematics,
Vol. 172,
Issue. 1,
p.
93.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2009.
Encyclopedia of Complexity and Systems Science.
p.
3055.
DOOLEY, ANTHONY H.
and
MORTISS, GENEVIEVE
2009.
On the critical dimensions of product odometers.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 2,
p.
475.
DOOLEY, ANTHONY H.
and
HAGIHARA, RIKA
2012.
Computing the critical dimensions of Bratteli–Vershik systems with multiple edges.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 1,
p.
103.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2012.
Mathematics of Complexity and Dynamical Systems.
p.
329.
MANSFIELD, DANIEL F.
and
DOOLEY, ANTHONY H.
2017.
The critical dimension for -measures.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 3,
p.
824.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2022.
Encyclopedia of Complexity and Systems Science.
p.
1.
Danilenko, Alexandre I.
and
Silva, Cesar E.
2023.
Ergodic Theory.
p.
233.


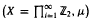 is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and
is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and 