Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-18T21:05:02.665Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of non-autonomous dissipative systems in Hilbert space

Part of: Differential equations in abstract spaces Special classes of linear operators

Published online by Cambridge University Press:  09 April 2009

Song Guozhu
Song Guozhu
Affiliation:
Department of Mathematics Nanjing UniversityNanjing 210008, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we discuss the asymptotic behaviour, as t → ∞, of the integral solution u(t) of the non-linear evolution equation 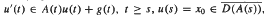where {A(t)}t≥0 is a family of m-dissipative operators in a Hilbert space H, and g ∈ Lloc (0, ∞ H).We give some sufficient conditions and some sufficient and necessary conditions to ensure that 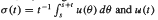are weakly convergent.

Keywords

Non-linear evolution equationdissipative operatorintegral solutionasymptotic behaviour

MSC classification

Secondary: 47B44: Accretive operators, dissipative operators, etc. 34G20: Nonlinear equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 62 , Issue 1 , February 1997 , pp. 93 - 103
Copyright
Copyright © Australian Mathematical Society 1997

References

[1]Barbu, V., Nonlinear semigroups and differential equations in Banach spaces (Nordhoff, Groningen, 1976).Google Scholar
[2]Brésis, H., Operateurs maximaux monotones (North-Holland, Amsterdam, 1973).Google Scholar
[3]Israel, M. M. Jr and Reich, S., ‘Asymptotic behavior of solutions of a nonlinear evolution equation’, J. Math. Anal. Appl. 83 (1981), 43–53.CrossRefGoogle Scholar
[4]Morosanu, G., ‘Asymptotic behaviour of solutions of differential equations associated to monotone operators’, Nonlinear Anal. 3 (1979), 873–883.Google Scholar
[5]Pavel, N. H., Nonlinear evolution operators and semigroups, Lecture Notes in Math. 1260 (Springer, Berlin, 1987).CrossRefGoogle Scholar
[6]Pazy, A., ‘Strong convergence of semigroups of nonlinear contractions in Hilbert space’, J. Analyse Math. 34 (1978), 1–35.CrossRefGoogle Scholar
[7]Pazy, A., ‘On the asymptotic behaviour of semigroups of nonlinear contractions in Hilbert space’, J. Funct. Anal. 27 (1978), 292–307.CrossRefGoogle Scholar
[8]Reich, S., ‘Nonlinear evolution equations and nonlinear ergodic theorems’, Nonlinear Anal. 1 (1977), 319–330.Google Scholar
[9]Reich, S., ‘Almost convergence and nonlinear ergodic theorems’, J. Approx. Theory 24 (1978), 269–272.Google Scholar
[10]Rouhani, B. D., ‘Asymptotic behaviour of quasi-autonomous dissipative systems in Hilbert spaces’, J. Math. Anal. Appl. 147 (1990), 465–476.CrossRefGoogle Scholar
[11]Guozhu, Song and Jipu, Ma, ‘Asymptotic behaviour of solutions to the nonlinear evolution equation’, Sci. China Ser. A 23 (1993), 679–686.Google Scholar