Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T09:27:03.966Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATE AMENABILITY OF SEGAL ALGEBRAS

Part of: Abstract harmonic analysis Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  18 July 2013

MAHMOOD ALAGHMANDAN
MAHMOOD ALAGHMANDAN*
Affiliation:
Department of Mathematics and Statistics, University of Saskatchewan, Saskatoon, Canada SK S7N 5E6 email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we first show that for a locally compact amenable group 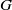$G$, every proper abstract Segal algebra of the Fourier algebra on 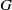$G$ is not approximately amenable; consequently, every proper Segal algebra on a locally compact abelian group is not approximately amenable. Then using the hypergroup generated by the dual of a compact group, it is shown that all proper Segal algebras of a class of compact groups including the 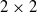$2\times 2$ special unitary group, 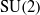$\mathrm{SU} (2)$, are not approximately amenable.

Keywords

approximately amenable Banach algebraSegal algebraabstract Segal algebralocally compact abelian groupcompact grouphypergroupLeptin condition

MSC classification

Secondary: 46H20: Structure, classification of topological algebras 43A20: $L^1$-algebras on groups, semigroups, etc. 43A62: Hypergroups 46H10: Ideals and subalgebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 1 , August 2013 , pp. 20 - 35
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bloom, W. R. and Heyer, H., Harmonic Analysis of Probability Measures on Hypergroups, de Gruyter Studies in Mathematics, 20 (Walter de Gruyter, Berlin, 1995).CrossRefGoogle Scholar
Burnham, J. T., ‘Closed ideals in subalgebras of Banach algebras. I’, Proc. Amer. Math. Soc. 32 (1972), 551–555.CrossRefGoogle Scholar
Choi, Y. and Ghahramani, F., ‘Approximate amenability of Schatten classes, Lipschitz algebras and second duals of Fourier algebras’, Q. J. Math. 62 (2011), 39–58.CrossRefGoogle Scholar
Dales, H. G. and Loy, R. J., ‘Approximate amenability of semigroup algebras and Segal algebras’, Dissertationes Math. (Rozprawy Mat.) 474 (2010), 58 pages.Google Scholar
Dunkl, C. F. and Ramirez, D. E., Topics in Harmonic Analysis, Appleton-Century Mathematics Series (Appleton-Century-Crofts, New York, 1971).Google Scholar
Eymard, P., ‘L’algébre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T. M., ‘Weak amenability of certain classes of Banach algebras without bounded approximate identities’, Math. Proc. Cambridge Philos. Soc. 133 (2002), 357–371.CrossRefGoogle Scholar
Ghahramani, F. and Loy, R. J., ‘Generalized notions of amenability’, J. Funct. Anal. 208 (1) (2004), 229–260.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. Vol. II: Structure and Analysis for Compact Groups. Analysis on Locally Compact Abelian Groups, Die Grundlehren der mathematischen Wissenschaften, 152 (Springer, New York–Berlin, 1970).Google Scholar
Hösel, V., Hofmann, M. and Lasser, R., ‘Means and Følner condition on polynomial hypergroups’, Mediterr. J. Math. 7 (1) (2010), 75–88.CrossRefGoogle Scholar
Kotzmann, E. and Rindler, H., ‘Segal algebras on nonabelian groups’, Trans. Amer. Math. Soc. 237 (1978), 271–281.CrossRefGoogle Scholar
Muruganandam, V., ‘Fourier algebra of a hypergroup. I’, J. Aust. Math. Soc. 82 (1) (2007), 59–83.Google Scholar
Pier, J. P., Amenable Locally Compact Groups, Pure and Applied Mathematics (Wiley, New York, 1984).Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Groups, 2nd edn, London Mathematical Society Monographs. New Series, 22 (Oxford University Press, New York, 2000).CrossRefGoogle Scholar
Rickart, C. E., General Theory of Banach Algebras, The University Series in Higher Mathematics (D. van Nostrand, Princeton, NJ–Toronto–London–New York, 1960).Google Scholar
Skantharajah, M., ‘Amenable hypergroups’, Illinois J. Math. 36 (1) (1992), 15–46.CrossRefGoogle Scholar
Vrem, R. C., ‘Harmonic analysis on compact hypergroups’, Pacific. J. Math. 85 (1979), 239–251.CrossRefGoogle Scholar