Article contents
Analysis of the effect of certain forcings on the nonoscillatory solutions of even order equations
Published online by Cambridge University Press: 09 April 2009
Abstract
Properties of solutions of 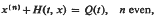 , are studied in the cause uH(t, u)>0 for u≠0. It is shown that two inequalities may always be associated with (I) in such a way that if one of these inequalities has a small positive solution and the other inequality has a small negative solution, then (I) is oscillatory. Further asymptotic properties of (I) are studied under assumptions involving intermediate antiderivatives P(i)(t), with P(n) = Q. Several results of this type ensure the non-existence of positive solutions of (I).
, are studied in the cause uH(t, u)>0 for u≠0. It is shown that two inequalities may always be associated with (I) in such a way that if one of these inequalities has a small positive solution and the other inequality has a small negative solution, then (I) is oscillatory. Further asymptotic properties of (I) are studied under assumptions involving intermediate antiderivatives P(i)(t), with P(n) = Q. Several results of this type ensure the non-existence of positive solutions of (I).
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 24 , Issue 2 , September 1977 , pp. 234 - 244
- Copyright
- Copyright © Australian Mathematical Society 1977
References
- 1
- Cited by


