Article contents
An improved bound for BFCp-groups
Published online by Cambridge University Press: 09 April 2009
Extract
The theme of this paper is a conjecture whose origins go back to work of B. H. Neumann ([5], Theorem 3·1) and his former students I. Wiegold and I. D. Macdonald ([7], [4]). B. H. Neumann proved that if there is a bound to the sizes of conjugacy classes in the group G. that is. if G is a BFC group. then the derived group G′ is finite; Wiegold. and later Macdonald. produced explicit upper bounds for G′ in terms of the maximum n of the sizes of the conjugacy classes in G. The coniecture is that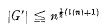 where l(n) should be the arithmetic function1 λ(n) for a best possible bound, or l(n) may be interpreted as log2n for a smooth, monotonicorderof-magnitude estimate. However, the bounds produced in [7] and [4], and even the vastly better upper bounds proved bv Sheooerd and Wieeold [6] for soluble groups, are very much bigger than
where l(n) should be the arithmetic function1 λ(n) for a best possible bound, or l(n) may be interpreted as log2n for a smooth, monotonicorderof-magnitude estimate. However, the bounds produced in [7] and [4], and even the vastly better upper bounds proved bv Sheooerd and Wieeold [6] for soluble groups, are very much bigger than 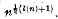 , and it is mv aim in this paper to take a first step towards closing the gap. This first, step is study of BFC p-groups: in a sequel I hope to show how the results proved here can be used to obtain improved bounds for arbitrary BFC groups.
, and it is mv aim in this paper to take a first step towards closing the gap. This first, step is study of BFC p-groups: in a sequel I hope to show how the results proved here can be used to obtain improved bounds for arbitrary BFC groups.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1970
References
- 12
- Cited by


