Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T07:59:43.471Z Has data issue: false hasContentIssue false
  • English
  • Français

RECOVERING THE BOUNDARY PATH SPACE OF A TOPOLOGICAL GRAPH USING POINTLESS TOPOLOGY

Part of: Distributive lattices Boolean algebras (Boolean rings) Selfadjoint operator algebras Basic constructions Topological dynamics

Published online by Cambridge University Press:  04 March 2020

GILLES G. DE CASTRO Open the ORCID record for GILLES G. DE CASTRO [Opens in a new window]
GILLES G. DE CASTRO*
Affiliation:
Departamento de Matemática, Centro de Ciências Físicas e Matemáticas, Universidade Federal de Santa Catarina, 88040-970Florianópolis SC, Brazil e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

First, we generalize the definition of a locally compact topology given by Paterson and Welch for a sequence of locally compact spaces to the case where the underlying spaces are 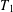$T_{1}$ and sober. We then consider a certain semilattice of basic open sets for this topology on the space of all paths on a graph and impose relations motivated by the definitions of graph C*-algebra in order to recover the boundary path space of a graph. This is done using techniques of pointless topology. Finally, we generalize the results to the case of topological graphs.

Keywords

topological graphsboundary path spacepointless topology

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 06D22: Frames, locales 37B10: Symbolic dynamics 54B05: Subspaces 54B10: Product spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 232 - 248
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by A. Sims

References

Boava, G., de Castro, G. G. and Mortari, F. de L., ‘Inverse semigroups associated with labelled spaces and their tight spectra’, Semigroup Forum 94(3) (2017), 582–609.Google Scholar
Cuntz, J. and Krieger, W., ‘A class of C ∗ -algebras and topological Markov chains’, Invent. Math. 56(3) (1980), 251–268.Google Scholar
Exel, R., ‘Inverse semigroups and combinatorial C ∗ -algebras’, Bull. Braz. Math. Soc. (N.S.) 39(2) (2008), 191–313.Google Scholar
Fowler, N. J., Laca, M. and Raeburn, I., ‘The C ∗ -algebras of infinite graphs’, Proc. Amer. Math. Soc. 128(8) (2000), 2319–2327.Google Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J. D., Mislove, M. and Scott, D. S., Continuous Lattices and Domains, Encyclopedia of Mathematics and its Applications, 93 (Cambridge University Press, Cambridge, 2003).Google Scholar
Johnstone, P. T., Stone Spaces, Cambridge Studies in Advanced Mathematics, 3 (Cambridge University Press, Cambridge, 1982).Google Scholar
Katsura, T., ‘A class of C ∗ -algebras generalizing both graph algebras and homeomorphism C ∗ -algebras. I. Fundamental results’, Trans. Amer. Math. Soc. 356(11) (2004), 4287–4322.Google Scholar
Kumjian, A. and Li, H., ‘Twisted topological graph algebras are twisted groupoid C ∗ -algebras’, J. Operator Theory 78(1) (2017), 201–225.Google Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids, and Cuntz–Krieger algebras’, J. Funct. Anal. 144(2) (1997), 505–541.Google Scholar
Lawson, M. V. and Lenz, D. H., ‘Pseudogroups and their étale groupoids’, Adv. Math. 244 (2013), 117–170.Google Scholar
Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding (Cambridge University Press, Cambridge, 1995).Google Scholar
Paterson, A. L. T., ‘Graph inverse semigroups, groupoids and their C ∗ -algebras’, J. Operator Theory 48(3, suppl.) (2002), 645–662.Google Scholar
Paterson, A. L. T. and Welch, A. E., ‘Tychonoff’s theorem for locally compact spaces and an elementary approach to the topology of path spaces’, Proc. Amer. Math. Soc. 133(9) (2005), 2761–2770.Google Scholar
Picado, J. and Pultr, A., Frames and Locales: Topology Without Points, Frontiers in Mathematics (Birkhäuser/Springer, Basel).Google Scholar
Renault, J., A Groupoid Approach to C ∗ -Algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin, 1980).Google Scholar
Resende, P., ‘Étale groupoids and their quantales’, Adv. Math. 208(1) (2007), 147–209.Google Scholar
Vickers, S., Topology Via Logic, Cambridge Tracts in Theoretical Computer Science, 5 (Cambridge University Press, Cambridge, 1989).Google Scholar
Webster, S. B. G., ‘The path space of a directed graph’, Proc. Amer. Math. Soc. 142(1) (2014), 213–225.Google Scholar
Yeend, T., ‘Groupoid models for the C ∗ -algebras of topological higher-rank graphs’, J. Operator Theory 57(1) (2007), 95–120.Google Scholar