Article contents
PERTURBATION THEOREMS FOR FRACTIONAL CRITICAL EQUATIONS ON BOUNDED DOMAINS
Published online by Cambridge University Press: 09 March 2020
Abstract
We consider the fractional critical problem 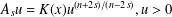 $A_{s}u=K(x)u^{(n+2s)/(n-2s)},u>0$ in
$A_{s}u=K(x)u^{(n+2s)/(n-2s)},u>0$ in 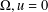 $\unicode[STIX]{x1D6FA},u=0$ on
$\unicode[STIX]{x1D6FA},u=0$ on 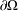 $\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$, where
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$, where 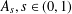 $A_{s},s\in (0,1)$, is the fractional Laplace operator and
$A_{s},s\in (0,1)$, is the fractional Laplace operator and 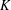 $K$ is a given function on a bounded domain
$K$ is a given function on a bounded domain  $\unicode[STIX]{x1D6FA}$ of
$\unicode[STIX]{x1D6FA}$ of 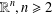 $\mathbb{R}^{n},n\geq 2$. This is based on A. Bahri’s theory of critical points at infinity in Bahri [Critical Points at Infinity in Some Variational Problems, Pitman Research Notes in Mathematics Series, 182 (Longman Scientific & Technical, Harlow, 1989)]. We prove Bahri’s estimates in the fractional setting and we provide existence theorems for the problem when
$\mathbb{R}^{n},n\geq 2$. This is based on A. Bahri’s theory of critical points at infinity in Bahri [Critical Points at Infinity in Some Variational Problems, Pitman Research Notes in Mathematics Series, 182 (Longman Scientific & Technical, Harlow, 1989)]. We prove Bahri’s estimates in the fractional setting and we provide existence theorems for the problem when 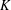 $K$ is close to 1.
$K$ is close to 1.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 159 - 178
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by F. Cirstea
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under Grant No. (KEP-PhD-41-130-38). The authors, therefore, acknowledge with thanks DSR technical and financial support.
References
- 4
- Cited by



