Article contents
CONDITION (K) FOR BOOLEAN DYNAMICAL SYSTEMS
Published online by Cambridge University Press: 27 May 2021
Abstract
We generalize Condition (K) from directed graphs to Boolean dynamical systems and show that a locally finite Boolean dynamical system 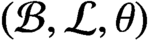 $({{\mathcal {B}}},{{\mathcal {L}}},\theta )$
with countable
$({{\mathcal {B}}},{{\mathcal {L}}},\theta )$
with countable 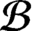 ${{\mathcal {B}}}$
and
${{\mathcal {B}}}$
and 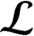 ${{\mathcal {L}}}$
satisfies Condition (K) if and only if every ideal of its
${{\mathcal {L}}}$
satisfies Condition (K) if and only if every ideal of its  $C^*$
-algebra is gauge-invariant, if and only if its
$C^*$
-algebra is gauge-invariant, if and only if its  $C^*$
-algebra has the (weak) ideal property, and if and only if its
$C^*$
-algebra has the (weak) ideal property, and if and only if its  $C^*$
-algebra has topological dimension zero. As a corollary we prove that if the
$C^*$
-algebra has topological dimension zero. As a corollary we prove that if the  $C^*$
-algebra of a locally finite Boolean dynamical system with
$C^*$
-algebra of a locally finite Boolean dynamical system with 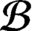 ${{\mathcal {B}}}$
and
${{\mathcal {B}}}$
and 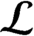 ${{\mathcal {L}}}$
countable either has real rank zero or is purely infinite, then
${{\mathcal {L}}}$
countable either has real rank zero or is purely infinite, then 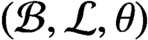 $({{\mathcal {B}}}, {{\mathcal {L}}}, \theta )$
satisfies Condition (K). We also generalize the notion of maximal tails from directed graph to Boolean dynamical systems and use this to give a complete description of the primitive ideal space of the
$({{\mathcal {B}}}, {{\mathcal {L}}}, \theta )$
satisfies Condition (K). We also generalize the notion of maximal tails from directed graph to Boolean dynamical systems and use this to give a complete description of the primitive ideal space of the  $C^*$
-algebra of a locally finite Boolean dynamical system that satisfies Condition (K) and has countable
$C^*$
-algebra of a locally finite Boolean dynamical system that satisfies Condition (K) and has countable 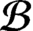 ${{\mathcal {B}}}$
and
${{\mathcal {B}}}$
and 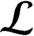 ${{\mathcal {L}}}$
.
${{\mathcal {L}}}$
.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc
Footnotes
Communicated by Aidan Sims
Research partially supported by NRF-2017R1D1A1B03030540.
References
- 3
- Cited by



