Article contents
2-LOCAL DERIVATIONS ON SEMISIMPLE BANACH ALGEBRAS WITH MINIMAL LEFT IDEALS
Published online by Cambridge University Press: 24 July 2020
Abstract
Let 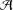 ${\mathcal{A}}$ be a semisimple Banach algebra with minimal left ideals and
${\mathcal{A}}$ be a semisimple Banach algebra with minimal left ideals and 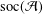 $\text{soc}({\mathcal{A}})$ be the socle of
$\text{soc}({\mathcal{A}})$ be the socle of 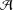 ${\mathcal{A}}$. We prove that if
${\mathcal{A}}$. We prove that if 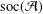 $\text{soc}({\mathcal{A}})$ is an essential ideal of
$\text{soc}({\mathcal{A}})$ is an essential ideal of 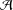 ${\mathcal{A}}$, then every 2-local derivation on
${\mathcal{A}}$, then every 2-local derivation on 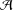 ${\mathcal{A}}$ is a derivation. As applications of this result, we can easily show that every 2-local derivation on some algebras, such as semisimple modular annihilator Banach algebras, strongly double triangle subspace lattice algebras and
${\mathcal{A}}$ is a derivation. As applications of this result, we can easily show that every 2-local derivation on some algebras, such as semisimple modular annihilator Banach algebras, strongly double triangle subspace lattice algebras and 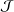 ${\mathcal{J}}$-subspace lattice algebras, is a derivation.
${\mathcal{J}}$-subspace lattice algebras, is a derivation.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by A. Sims
This paper was partially supported by the National Natural Science Foundation of China (Grant No. 11871021).
References
- 1
- Cited by



