Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T08:44:09.163Z Has data issue: false hasContentIssue false
  • English
  • Français

2-ARC-TRANSITIVE REGULAR COVERS OF 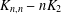$K_{n,n}-nK_{2}$ HAVING THE COVERING TRANSFORMATION GROUP 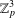$\mathbb{Z}_{p}^{3}$

Part of: Algebraic combinatorics Permutation groups Graph theory

Published online by Cambridge University Press:  16 March 2016

SHAOFEI DU  and
WENQIN XU
SHAOFEI DU*
Affiliation:
School of Mathematical Sciences, Capital Normal University, Beijing 100048, PR China email [email protected]
WENQIN XU
Affiliation:
School of Mathematical Sciences, Capital Normal University, Beijing 100048, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

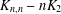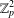This paper contributes to the regular covers of a complete bipartite graph minus a matching, denoted $K_{n,n}-nK_{2}$, whose fiber-preserving automorphism group acts 2-arc-transitively. All such covers, when the covering transformation group $K$ is either cyclic or $\mathbb{Z}_{p}^{2}$ with 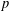$p$ a prime, have been determined in Xu and Du [‘2-arc-transitive cyclic covers of 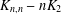$K_{n,n}-nK_{2}$’, J. Algebraic Combin.39 (2014), 883–902] and Xu et al. [‘2-arc-transitive regular covers of 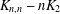$K_{n,n}-nK_{2}$ with the covering transformation group 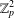$\mathbb{Z}_{p}^{2}$’, Ars. Math. Contemp.10 (2016), 269–280]. Finally, this paper gives a classification of all such covers for 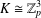$K\cong \mathbb{Z}_{p}^{3}$ with 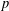$p$ a prime.

Keywords

arc-transitive graphcovering graphlifting2-transitive group

MSC classification

Primary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures 05E30: Association schemes, strongly regular graphs
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 2 , October 2016 , pp. 145 - 170
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Bloom, D. M., ‘The subgroups of PSL(3, q) for odd q ’, Trans. Amer. Math. Soc. 127 (1967), 150–178.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997), 235–265.Google Scholar
Cameron, P. J., ‘Finite permutation groups and finite simple groups’, Bull. Lond. Math. Soc. 13 (1981), 1–22.Google Scholar
Cameron, P. J. and Kantor, W. M., ‘2-Transitive and antiflag transitive collineation groups of finite projective spaces’, J. Algebra 60 (1979), 384–422.CrossRefGoogle Scholar
Conder, M. D. E. and Ma, J., ‘Arc-transitive abelian regular covers of cubic graphs’, J. Algebra 387 (2013), 215–242.Google Scholar
Conder, M. D. E. and Ma, J., ‘Arc-transitive abelian regular covers of the Heawood graph’, J. Algebra 387 (2013), 243–267.Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups (Clarendon Press, Oxford, 1985).Google Scholar
Du, S. F., Kwak, J. H. and Xu, M. Y., ‘On 2-arc-transitive covers of complete graphs with covering transformation group ℤ p 3 ’, J. Combin. Theory B 93 (2005), 73–93.Google Scholar
Du, S. F., Malnič, A. and Marušič, D., ‘Classification of 2-arc-transitive dihedrants’, J. Combin. Theory B 98 (2008), 1349–1372.Google Scholar
Du, S. F., Marušič, D. and Waller, A. O., ‘On 2-arc-transitive covers of complete graphs’, J. Combin. Theory B 74 (1998), 276–290.Google Scholar
Du, S. F. and Xu, M. Y., ‘A classification of semisymmetric graphs of order 2pq ’, Comm. Algebra 28 (2000), 2685–2715.CrossRefGoogle Scholar
Fang, X. G., Havas, G. and Praeger, C. E., ‘On the automorphism groups of quasiprimitive almost simple graphs’, J. Algebra 222 (1999), 271–283.Google Scholar
Fang, X. G. and Praeger, C. E., ‘Finite two-arc-transitive graphs admitting a Suzuki simple group’, Comm. Algebra 27 (1999), 3727–3754.CrossRefGoogle Scholar
Gardiner, A. and Praeger, C. E., ‘Topological covers of complete graphs’, Math. Proc. Cambridge Philos. Soc. 123 (1998), 549–559.CrossRefGoogle Scholar
Godsil, C. D. and Hensel, A. D., ‘Distance regular covers of the complete graph’, J. Combin. Theory B 56 (1992), 205–238.CrossRefGoogle Scholar
Godsil, C. D., Liebler, R. A. and Praeger, C. E., ‘Antiposal distance transitive covers of complete graphs’, European J. Combin. 19 (1992), 455–478.Google Scholar
Gross, J. L. and Tucker, T. W., ‘Generating all graph coverings by permutation voltage assignments’, Discrete Math. 18 (1977), 273–283.Google Scholar
Gross, J. L. and Tucker, T. W., Topological Graph Theory (Wiley-Interscience, New York, 1987).Google Scholar
Hall, M. and Senior, J. K., The Groups of Order 2 n (n ≤ 6) (Macmillan, New York, 1964).Google Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin, 1967).Google Scholar
Ivanov, A. A. and Praeger, C. E., ‘On finite affine 2-arc-transitive graphs’, European J. Combin. 14 (1993), 421–444.Google Scholar
Li, C. H., ‘On finite s-transitive graphs of odd order’, J. Combin. Theory B 81 (2001), 307–317.Google Scholar
Li, C. H., ‘The finite vertex-primitive and vertex-biprimitive s-transitive graphs for s ≥ 4’, Trans. Amer. Math. Soc. 353 (2001), 3511–3529.CrossRefGoogle Scholar
Lorimer, P., ‘Vertex-transitive graphs: symmetric graphs of prime valency’, J. Graph Theory 8 (1984), 55–68.Google Scholar
Malnič, A., ‘Group actions, coverings and lifts of automorphisms’, Discrete Math. 182 (1998), 203–218.Google Scholar
Marušič, D., ‘On 2-arc-transitivity of Cayley graphs’, J. Combin. Theory B 87 (2003), 162–196.CrossRefGoogle Scholar
Mortimer, B., ‘The modular permutation representations of the known doubly transitive groups’, Proc. Lond. Math. Soc. 41 (1980), 1–20.Google Scholar
Praeger, C. E., ‘An O’Nan–Scott theorem for finite quasiprimitive permutation groups and an application to 2-arc-transitive graphs’, J. Lond. Math. Soc. 47 (1993), 227–239.Google Scholar
Praeger, C. E., ‘On a reduction theorem for finite, bipartite, 2-arc-transitive graphs’, Australas. J. Combin. 7 (1993), 21–36.Google Scholar
Wang, F. R. and Zhang, L., ‘Elementary Abelian regular coverings of cube’, Int. J. Math. Combin. 1 (2011), 49–58.Google Scholar
Xu, W. Q. and Du, S. F., ‘2-arc-transitive cyclic covers of K n, n - nK 2 ’, J. Algebraic Combin. 39 (2014), 883–902.Google Scholar
Xu, W. Q., Du, S. F., Kwak, J. H. and Xu, M. Y., ‘2-arc-transitive metacyclic covers of complete graphs’, J. Combin. Theory B 111 (2015), 54–74.Google Scholar
Xu, W. Q., Zhu, Y. H. and Du, S. F., ‘2-arc-transitive regular covers of K n, n - nK 2 with the covering transformation group ℤ p 2 ’, Ars Math. Contemp. 10 (2016), 269–280.Google Scholar